
–Ъ–ї–∞—Б—Б–Є—Д–Є–Ї–∞—В–Њ—А –љ–∞ –Њ—Б–љ–Њ–≤–µ RBF.
–Х–≤–≥–µ–љ–Є–є –С–Њ—А–Є—Б–Њ–≤ —З–µ—В–≤–µ—А–≥, 26 –і–µ–Ї–∞–±—А—П 2013 –≥.–Т —Н—В–Њ–є —Б—В–∞—В—М–µ –Њ–њ–Є—Б—Л–≤–∞–µ—В—Б—П –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—В–Њ—А –љ–∞ –Њ—Б–љ–Њ–≤–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є –Љ–Њ–і–µ–ї–Є, –Ї–Њ—В–Њ—А–∞—П –љ–Њ—Б–Є—В –љ–∞–Ј–≤–∞–љ–Є–µ —Б–µ—В—М —А–∞–і–Є–∞–ї—М–љ—Л—Е –±–∞–Ј–Є—Б–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є (RBF).
1 –°–µ—В—М —А–∞–і–Є–∞–ї—М–љ—Л—Е –±–∞–Ј–Є—Б–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є
–°–µ—В—М —А–∞–і–Є–∞–ї—М–љ—Л—Е –±–∞–Ј–Є—Б–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є, RBF –Є–ї–Є –≥–∞—Г—Б—Б–Њ–≤–∞ —Б–Љ–µ—Б—М —Н—В–Њ –Њ–і–Є–љ –Є–Ј –≤–∞—А–Є–∞–љ—В–Њ–≤ –±–∞–є–µ—Б–Њ–≤—Б–Ї–Њ–≥–Њ –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—В–Њ—А–∞.
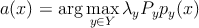 | (1) |
–≥–і–µ y вИИ Y - –љ–Њ–Љ–µ—А –Ї–ї–∞—Б—Б–∞, ќїy вАУ –њ–Њ—В–µ—А—П –њ—А–Є –Њ—И–Є–±–Њ—З–љ–Њ–є –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є–Є –і–ї—П –Ї–ї–∞—Б—Б–∞ y, Py вАУ –∞–њ—А–Є–Њ—А–љ–∞—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Ї–ї–∞—Б—Б–∞ y (–Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –і–Њ–ї–µ–є –Њ–±—К–µ–Ї—В–Њ–≤ xy –Ї–ї–∞—Б—Б–∞ y –≤ –Њ–±—Й–µ–Љ –љ–∞–±–Њ—А–µ X), py(x) вАУ –њ–ї–Њ—В–љ–Њ—Б—В—М —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П xy –Є–Ј –Ї–ї–∞—Б—Б–∞ y.
–Ч–і–µ—Б—М –њ–ї–Њ—В–љ–Њ—Б—В—М —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П py(x) –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Ї–∞–Ї —Б–Љ–µ—Б—М –Љ–љ–Њ–≥–Њ–Љ–µ—А–љ—Л–є –љ–Њ—А–Љ–∞–ї—М–љ—Л—Е (–≥–∞—Г—Б—Б–Њ–≤—Б–Ї–Є—Е) –њ–ї–Њ—В–љ–Њ—Б—В–µ–є.
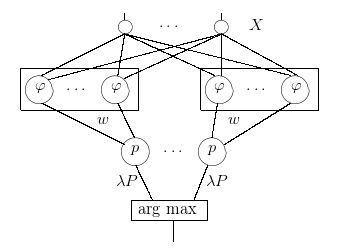
–†–Є—Б.1: –љ–µ–є—А–Њ–љ–љ–∞—П —Б–µ—В—М RBF
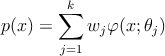
–≥–і–µ k - –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В —Б–Љ–µ—Б–Є, wj - –≤–µ—Б–Њ–≤–Њ–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В (–∞–њ—А–Є–Њ—А–љ–∞—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Ї–Њ–Љ–њ–Њ–љ–µ–љ—В—Л), ѕЖ(x; 𝜃j) - –љ–Њ—А–Љ–∞–ї—М–љ–∞—П –њ–ї–Њ—В–љ–Њ—Б—В—М.
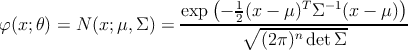
–Ј–і–µ—Б—М ќЉ - –Љ–∞—В.–Њ–ґ–Є–і–∞–љ–Є–µ (—Ж–µ–љ—В—А) X, ќ£ –Љ–∞—В—А–Є—Ж–∞ –Ї–Њ–≤–∞—А–Є–∞—Ж–Є–є X .
RBF –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –≤ –≤–Є–і–µ –љ–µ–є—А–Њ–љ–љ–Њ–є —Б–µ—В–Є (—А–Є—Б.1).
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –љ–∞–±–Њ—А –Њ–і–љ–Њ—В–Є–њ–љ—Л—Е —Г—З–µ–±–љ—Л—Е –Љ–љ–Њ–ґ–µ—Б—В–≤
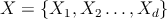
2 –†–µ–∞–ї–Є–Ј–∞—Ж–Є—П
–Т —Н—В–Њ–Љ —А–∞–Ј–і–µ–ї–µ –Љ—Л —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —А–µ–∞–ї–Є–Ј–∞—Ж–Є–Є –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—В–Њ—А–∞ –љ–∞ –Њ—Б–љ–Њ–≤–µ RBF –і–ї—П —В–Њ—З–µ–Ї –љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є (n = 2)
–Э–∞ —А–Є—Б—Г–љ–Ї–∞—Е –љ–Є–ґ–µ –њ—А–Њ–Є–ї–ї—О—Б—В—А–Є—А–Њ–≤–∞–љ–∞ —А–µ–Ј—Г–ї—М—В–∞—В—Л —А–∞–±–Њ—В—Л RBF-–Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—В–Њ—А–∞.
 |
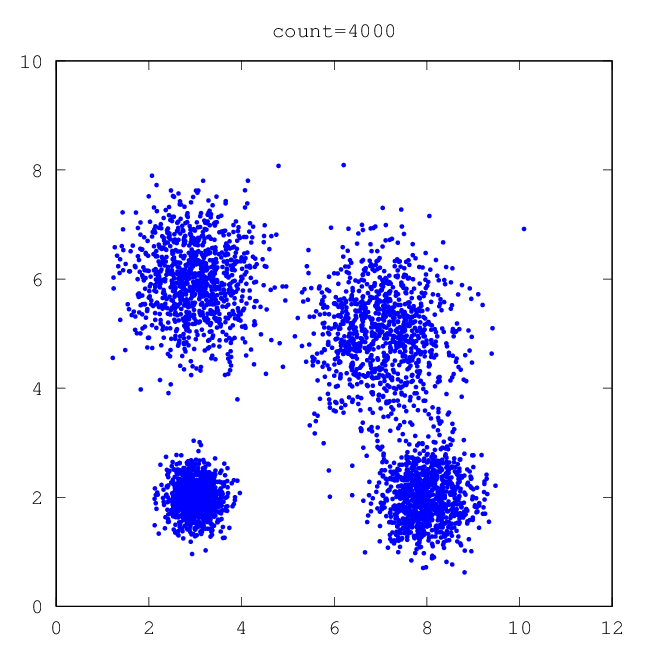 |
| –†–Є—Б.2: —Г—З–µ–±–љ—Л–є –љ–∞–±–Њ—А | –†–Є—Б.3: —В–µ—Б—В |
| | |
 |
|
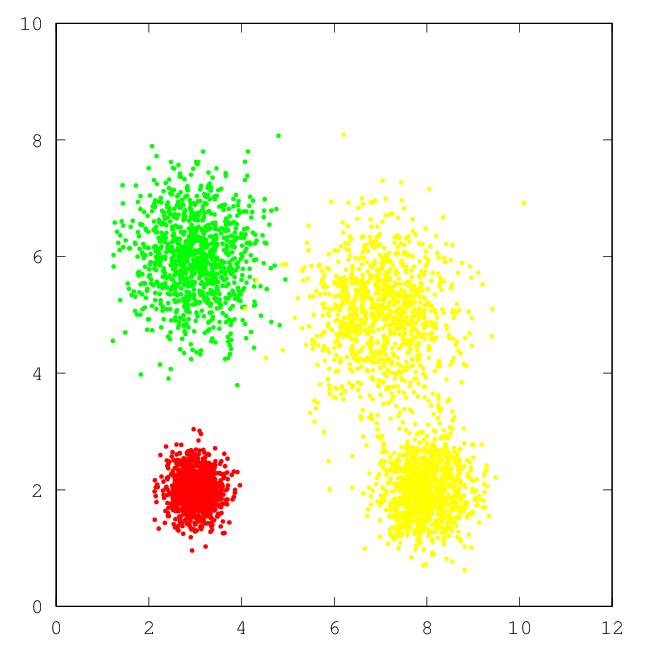
| –†–Є—Б.4: —А–µ–Ј—Г–ї—М—В–∞—В —А–∞–±–Њ—В—Л RBF | |
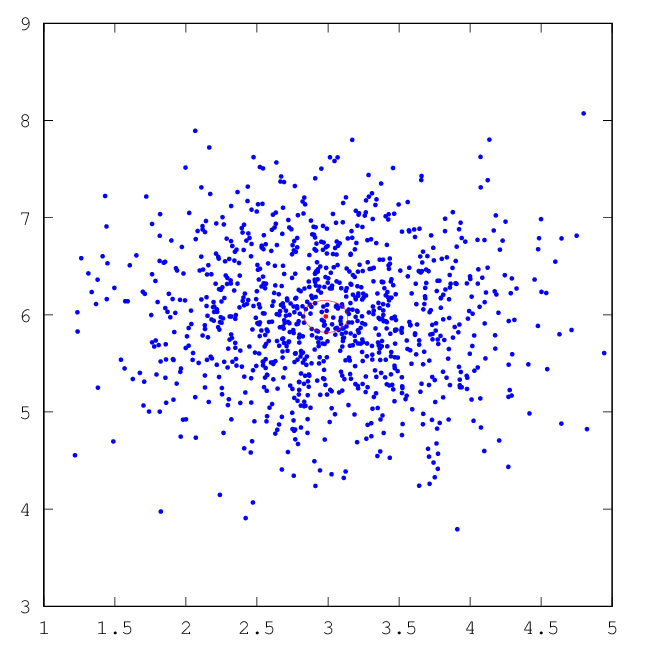
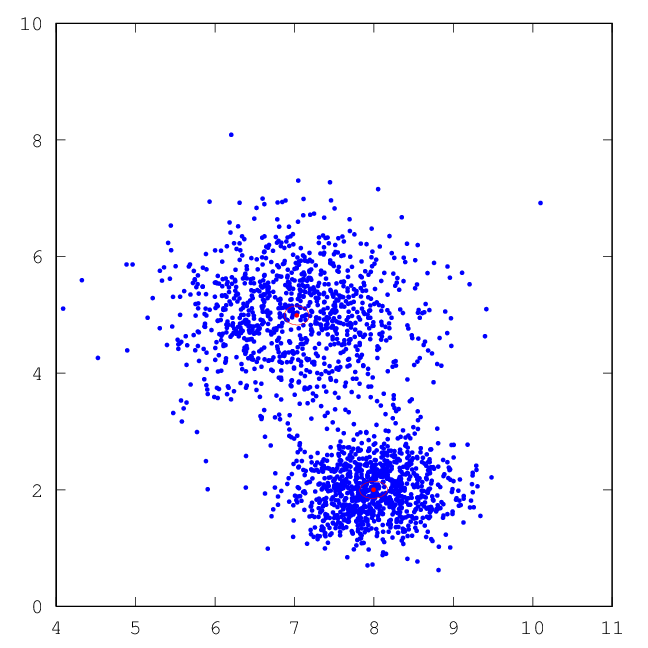
–Э–∞ —А–Є—Б—Г–љ–Ї–∞—Е –љ–Є–ґ–µ –њ—А–Њ–Є–ї–ї—О—Б—В—А–Є—А–Њ–≤–∞–љ–∞ —А–∞–±–Њ—В–∞ –Х–Ь-–∞–ї–≥–Њ—А–Є—В–Љ–∞, –Ї–Њ—В–Њ—А—Л–є –≤–Њ—Б—Б—В–∞–љ–∞–≤–ї–Є–≤–∞–µ—В —Б–Љ–µ—Б—М –њ–ї–Њ—В–љ–Њ—Б—В–µ–є.
| | |
 |
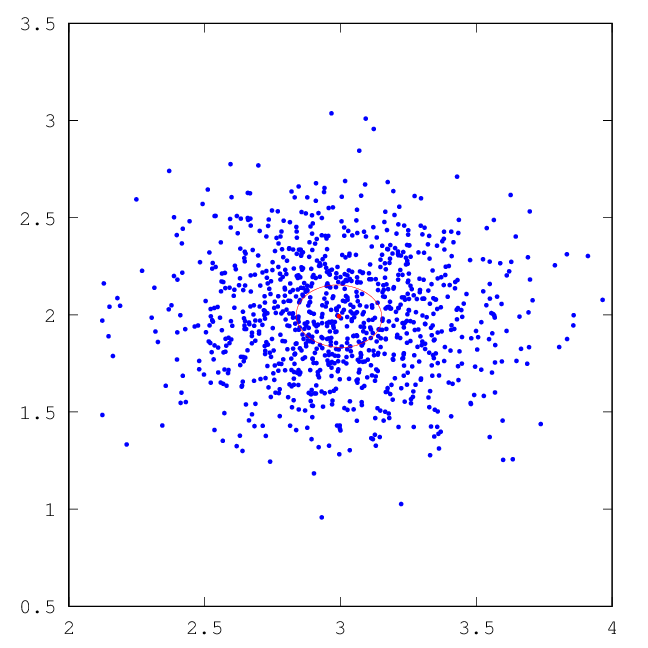 |
| –†–Є—Б.5: —А–µ–Ј—Г–ї—М—В–∞—В –Х–Ь –і–ї—П –њ–µ—А–≤–Њ–≥–Њ –Ї–ї–∞—Б—Б–∞ | –†–Є—Б.6: —А–µ–Ј—Г–ї—М—В–∞—В –Х–Ь –і–ї—П –≤—В–Њ—А–Њ–≥–Њ –Ї–ї–∞—Б—Б–∞ |
| | |
 |
|
| –†–Є—Б.7: —А–µ–Ј—Г–ї—М—В–∞—В –Х–Ь –і–ї—П —В—А–µ—В—М–µ–≥–Њ –Ї–ї–∞—Б—Б–∞ | |
–†–µ–∞–ї–Є–Ј–∞—Ж–Є—П –≤ —Б–Є—Б—В–µ–Љ–µ Octave [ –Ј–і–µ—Б—М ].
–°–њ–Є—Б–Њ–Ї –ї–Є—В–µ—А–∞—В—Г—А—Л
[1] –Т–Њ—А–Њ–љ—Ж–Њ–≤ –Ъ.–Т. –°—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Є–µ –Љ–µ—В–Њ–і—Л –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є–Є вАУ http://shad.yandex.ru/lectures/machine_learning.xml
