–£–Ψ―¹―¹―²–Α–Ϋ–Ψ–≤–Μ–Β–Ϋ–Η–Β ―¹–Φ–Β―¹–Η –Ω–Μ–Ψ―²–Ϋ–Ψ―¹―²–Β–Ι ―Ä–Α―¹–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η–Ι ―¹ –Ω–Ψ–Φ–Ψ―â―¨―é EM-–Α–Μ–≥–Ψ―Ä–Η―²–Φ–Α.
–ï–≤–≥–Β–Ϋ–Η–Ι –ë–Ψ―Ä–Η―¹–Ψ–≤ ―΅–Β―²–≤–Β―Ä–≥, 26 –¥–Β–Κ–Α–±―Ä―è 2013 –≥.–£ ―ç―²–Ψ–Ι ―¹―²–Α―²―¨–Β –Φ―΄ –Ω–Ψ–≥–Ψ–≤–Ψ―Ä–Η–Φ –Ψ –Ζ–Α–¥–Α―΅–Β –≤–Ψ―¹―¹―²–Α–Ϋ–Ψ–≤–Μ–Β–Ϋ–Η―è ―¹–Φ–Β―¹–Η –Ω–Μ–Ψ―²–Ϋ–Ψ―¹―²–Β–Ι ―Ä–Α―¹–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η–Ι ―²–Ψ―΅–Β–Κ –Η –Ψ –Φ–Β―²–Ψ–¥–Β, –Κ–Ψ―²–Ψ―Ä―΄–Ι –Ϋ–Α–Ζ―΄–≤–Α–Β―²―¹―è EM-–Α–Μ–≥–Ψ―Ä–Η―²–Φ (expectationβÄ™maximization algorithm). –≠―²–Ψ―² –Φ–Β―²–Ψ–¥ –Φ–Ψ–Ε–Ϋ–Ψ –Ω―Ä–Η–Φ–Β–Ϋ―è―²―¨ –¥–Μ―è ―Ä–Β―à–Β–Ϋ–Η―è ―Ä–Α–Ζ–Ϋ―΄―Ö –Ω―Ä–Α–Κ―²–Η―΅–Β―¹–Κ–Η―Ö –Ζ–Α–¥–Α―΅, –Ϋ–Α–Ω―Ä–Η–Φ–Β―Ä –¥–Μ―è ―Ä–Β―à–Β–Ϋ–Η―è –Ζ–Α–¥–Α―΅–Η –Κ–Μ–Α―¹―²–Β―Ä–Η–Ζ–Α―Ü–Η–Η.
1 –£–≤–Β–¥–Β–Ϋ–Η–Β
–†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ –Φ–Ϋ–Ψ–Ε–Β―¹―²–≤–Ψ ―²–Ψ―΅–Β–Κ X, –Ω–Ψ―ç―²–Ψ–Φ―É –Ϋ–Α–±–Ψ―Ä―É ―²–Ψ―΅–Β–Κ ―²―Ä–Β–±―É–Β―²―¹―è –≤–Ψ―¹―¹―²–Α–Ϋ–Ψ–≤–Η―²―¨ –Ω–Μ–Ψ―²–Ϋ–Ψ―¹―²―¨ –Η―Ö ―Ä–Α―¹–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―è. –ü―É―¹―²―¨ –Ω–Μ–Ψ―²–Ϋ–Ψ―¹―²―¨ –Η–Φ–Β–Β―² ―¹–Μ–Β–¥―É―é―â–Η–Ι –≤–Η–¥
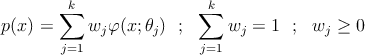
–½–Α–¥–Α―΅–Α: –Ϋ–Α–Ι―²–Η –Ψ–Ω―²–Η–Φ–Α–Μ―¨–Ϋ―΄–Β 𝜃j,wj –Ω–Ψ –Ω―Ä–Ψ―¹―²–Ψ–Ι –≤―΄–±–Ψ―Ä–Κ–Β X –Η –Ζ–Α–¥–Α–Ϋ–Ϋ―΄–Φ k –Η œÜ.
2 –ë–Α–Ζ–Ψ–≤―΄–Ι –≤–Α―Ä–Η–Α–Ϋ―² EM-–Α–Μ–≥–Ψ―Ä–Η―²–Φ–Α
–î–Μ―è ―Ä–Β―à–Β–Ϋ–Η―è –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤―΄―à–Β –Ζ–Α–¥–Α―΅–Η –Φ–Ψ–Ε–Ϋ–Ψ –Η―¹–Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α―²―¨ EM-–Α–Μ–≥–Ψ―Ä–Η―²–Φ, –Κ–Ψ―²–Ψ―Ä―΄–Ι ―¹–Ψ―¹―²–Ψ–Η―² –Η–Ζ –¥–≤―É―Ö –Ψ―¹–Ϋ–Ψ–≤–Ϋ―΄―Ö –Ω―Ä–Ψ―Ü–Β–¥―É―Ä: E-―à–Α–≥ - –Ψ―Ü–Β–Ϋ–Κ–Α –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–≤ –Η –€-–®–Α–≥ - –Ψ–Ω―²–Η–Φ–Η–Ζ–Α―Ü–Η―è –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–≤. –ë–Α–Ζ–Ψ–≤―΄–Ι –≤–Α―Ä–Η–Α–Ϋ―² EM-–Α–Μ–≥–Ψ―Ä–Η―²–Φ–Α –≤―΄–≥–Μ―è–¥–Η―² ―¹–Μ–Β–¥―É―é―â–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ.
- –≤―΄–±―Ä–Α―²―¨ –Ϋ–Α―΅–Α–Μ―¨–Ϋ―΄–Β –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è w –Η 𝜃
- stepE: –≤―΄―΅–Η―¹–Μ–Η―²―¨ –Ψ―Ü–Β–Ϋ–Κ―É –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–≤
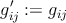
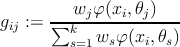
i = 1,βÄΠ,m - –Ϋ–Ψ–Φ–Β―Ä –Ψ–±―ä–Β–Κ―²–Α –≤ –≤―΄–±–Ψ―Ä–Κ–Β,
j = 1,βÄΠ,k - –Ϋ–Ψ–Φ–Β―Ä –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²―΄ ―¹–Φ–Β―¹–Η ―Ä–Α―¹–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―è - stepM: –Ψ–Ω―²–Η–Φ–Η–Ζ–Η―Ä–Ψ–≤–Α―²―¨ –Ω–Α―Ä–Α–Φ–Β―²―Ä―΄
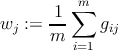
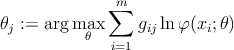
(1) - –Β―¹–Μ–Η max i,j|gij β࣠gβÄ≤ij| > Έ¥
―²–Ψ –Ω–Β―Ä–Β―Ö–Ψ–¥ –Ϋ–Α –Ω.2–≥–¥–Β 0 < Έ¥ < 1 βÄ™ –Φ–Α–Κ―¹–Η–Φ–Α–Μ―¨–Ϋ–Ψ–Β –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β –Η–Ζ–Φ–Β–Ϋ–Β–Ϋ–Η―è –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–≤ (―É―¹–Μ–Ψ–≤–Η–Β –Ψ―¹―²–Α–Ϋ–Ψ–≤–Κ–Η EM)
- –Κ–Ψ–Ϋ–Β―Ü
–≠―²–Ψ –±–Α–Ζ–Ψ–≤―΄–Ι –≤–Α―Ä–Η–Α–Ϋ―² –Φ–Β―²–Ψ–¥–Α. –†–Β–Ζ―É–Μ―¨―²–Α―² –Β–≥–Ψ ―Ä–Α–±–Ψ―²―΄ –Ζ–Α–≤–Η―¹–Η―² –Ψ―² –Ϋ–Α―΅–Α–Μ―¨–Ϋ―΄―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Ι –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–≤, –Ζ–¥–Β―¹―¨ –Ϋ–Β –≤–Ω–Ψ–Μ–Ϋ–Β ―è―¹–Ϋ–Ψ –Κ–Α–Κ –≤―΄–±–Η―Ä–Α―²―¨ –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Ψ –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―² k –Η –Ϋ–Α―΅–Α–Μ―¨–Ϋ―΄–Β –Ω–Α―Ä–Α–Φ–Β―²―Ä―΄ 𝜃j. –î–Μ―è ―Ä–Β―à–Β–Ϋ–Η―è ―ç―²–Η―Ö –Ζ–Α–¥–Α―΅ ―¹―É―â–Β―¹―²–≤―É–Β―² –Φ–Ψ–¥–Η―³–Η–Κ–Α―Ü–Η―è –±–Α–Ζ–Ψ–≤–Ψ–≥–Ψ –Α–Μ–≥–Ψ―Ä–Η―²–Φ–Α - EM-–Α–Μ–≥–Ψ―Ä–Η―²–Φ ―¹ –Ω–Ψ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ―΄–Φ –¥–Ψ–±–Α–≤–Μ–Β–Ϋ–Η–Β–Φ –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―².
3 EM-–Α–Μ–≥–Ψ―Ä–Η―²–Φ ―¹ –Ω–Ψ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ―΄–Φ –¥–Ψ–±–Α–≤–Μ–Β–Ϋ–Η–Β–Φ –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²
–‰–¥–Β―è ―ç―²–Ψ–Ι –Φ–Ψ–¥–Η―³–Η–Κ–Α―Ü–Η–Η –ï–€-–Α–Μ–≥–Ψ―Ä–Η―²–Φ–Α –≤–Ω–Ψ–Μ–Ϋ–Β –Ψ–Ω–Η―¹―΄–≤–Α–Β―²―¹―è –≤ –Ϋ–Α–Ζ–≤–Α–Ϋ–Η–Η. –€―΄ –Ω–Ψ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ –¥–Ψ–±–Α–≤–Μ―è–Β–Φ –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²―΄ –Κ ―¹–Φ–Β―¹–Η, –Ϋ–Α –Κ–Α–Ε–¥–Ψ–Φ ―à–Α–≥–Β –≤―΄–Ω–Ψ–Μ–Ϋ―è–Β–Φ –±–Α–Ζ–Ψ–≤―΄–Ι –ï–€ –Η –Ψ―Ü–Β–Ϋ–Η–≤–Α–Β–Φ –Κ–Α―΅–Β―¹―²–≤–Ψ ―Ä–Β–Ζ―É–Μ―¨―²–Α―²–Α –Ω–Ψ –Ψ–Ω―Ä–Β–¥–Β–Μ―ë–Ϋ–Ϋ–Ψ–Ι –Ω―Ä–Ψ―Ü–Β–¥―É―Ä–Β. –≠―²–Ψ―² –≤–Α―Ä–Η–Α–Ϋ―² EM-–Α–Μ–≥–Ψ―Ä–Η―²–Φ–Α –≤―΄–≥–Μ―è–¥–Η―² ―¹–Μ–Β–¥―É―é―â–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ.
- –≤―΄–±―Ä–Α―²―¨ –Ϋ–Α―΅–Α–Μ―¨–Ϋ―΄–Β –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–≤
k = 1, w = 1
–Ω–Α―Ä–Α–Φ–Β―²―Ä―΄ 𝜃 –≤―΄–±–Η―Ä–Α―é―²―¹―è –≤ –Ζ–Α–≤–Η―¹–Η–Φ–Ψ―¹―²–Η –Ψ―² –≤–Η–¥–Α ―³―É–Ϋ–Κ―Ü–Η–Η œÜ,
–Ϋ–Α–Ω―Ä–Η–Φ–Β―Ä, –Β―¹–Μ–Η œÜ ―ç―²–Ψ –Φ–Ϋ–Ψ–≥–Ψ–Φ–Β―Ä–Ϋ–Α―è –Ϋ–Ψ―Ä–Φ–Α–Μ―¨–Ϋ–Α―è (–≥–Α―É―¹―¹–Ψ–≤―¹–Κ–Α―è) –Ω–Μ–Ψ―²–Ϋ–Ψ―¹―²―¨
―²–Ψ 𝜃1 = (w1,ΈΦ1, ΈΘ1), –≥–¥–Β ΈΦ1 - –Φ–Α―².–Ψ–Ε–Η–¥–Α–Ϋ–Η–Β, ΈΘ1 - –Φ–Α―²―Ä–Η―Ü–Α –Κ–Ψ–≤–Α―Ä–Η–Α―Ü–Η–Ι –Ϋ–Α X. - –Ϋ–Α–Ι―²–Η –Φ–Α–Κ―¹–Η–Φ–Α–Μ―¨–Ϋ–Ψ–Β –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β –Ω–Μ–Ψ―²–Ϋ–Ψ―¹―²–Η p –Ϋ–Α X
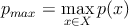
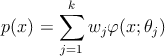
- –≤―΄–±―Ä–Α―²―¨ –Η–Ζ X ―²–Ψ―΅–Κ–Η ―¹ –Ω–Μ–Ψ―²–Ϋ–Ψ―¹―²―¨―é –Ϋ–Η–Ε–Β –Ω–Ψ―Ä–Ψ–≥–Ψ–≤–Ψ–Ι R β΄Ö pmax,
–≥–¥–Β 0 < R < 1 βÄ™ –Κ–Ψ―ç―³―³–Η―Ü–Η–Β–Ϋ―² –Ω―Ä–Α–≤–¥–Ψ–Ω–Ψ–¥–Ψ–±–Η―è
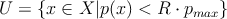
- –Β―¹–Μ–Η |U| < m0
―²–Ψ –Ω–Β―Ä–Β―Ö–Ψ–¥ –Ϋ–Α –Ω.8–≥–¥–Β 0 < m0 < |X| βÄ™ –Φ–Η–Ϋ–Η–Φ–Α–Μ―¨–Ϋ–Α―è –¥–Μ–Η–Ϋ–Ϋ–Α –≤―΄–±–Ψ―Ä–Κ–Η –¥–Μ―è –Ψ–±―Ä–Α–±–Ψ―²–Κ–Η
- –¥–Ψ–±–Α–≤–Μ―è–Β–Φ –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²―É ―¹–Φ–Β―¹–Η
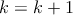
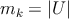
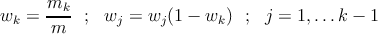
–Ω–Α―Ä–Α–Φ–Β―²―Ä―΄ –¥–Μ―è –Ϋ–Ψ―Ä–Φ–Α–Μ―¨–Ϋ–Ψ–Ι (–≥–Α―É―¹―¹–Ψ–≤―¹–Κ–Ψ–Ι) –Ω–Μ–Ψ―²–Ϋ–Ψ―¹―²–Η œÜ
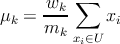
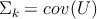
- –≤―΄–Ω–Ψ–Μ–Ϋ―è–Β–Φ –±–Α–Ζ–Ψ–≤―É―é –Ω―Ä–Ψ―Ü–Β–¥―É―Ä―É –Ψ–Ω―²–Η–Φ–Η–Ζ–Α―Ü–Η–Η
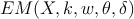
–≥–¥–Β 0 < Έ¥ < 1 - –Φ–Α–Κ―¹–Η–Φ–Α–Μ―¨–Ϋ–Ψ–Β –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β –Η–Ζ–Φ–Β–Ϋ–Β–Ϋ–Η―è –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–≤(―É―¹–Μ–Ψ–≤–Η–Β –Ψ―¹―²–Α–Ϋ–Ψ–≤–Κ–Η EM)
- –Ω–Β―Ä–Β―Ö–Ψ–¥ –Ϋ–Α –Ω.2
- –Κ–Ψ–Ϋ–Β―Ü
4 –†–Β–Α–Μ–Η–Ζ–Α―Ü–Η―è
–£ ―ç―²–Ψ–Φ ―Ä–Α–Ζ–¥–Β–Μ–Β –Φ―΄ ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―Ä–Β–Α–Μ–Η–Ζ–Α―Ü–Η–Η –±–Α–Ζ–Ψ–≤–Ψ–≥–Ψ –Η –Ω–Ψ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ–≥–Ψ EM-–Α–Μ–≥–Ψ―Ä–Η―²–Φ–Ψ–≤ –¥–Μ―è ―²–Ψ―΅–Β–Κ –Ϋ–Α –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Η (n = 2).
–û–Ω―Ä–Β–¥–Β–Μ–Η–Φ œÜ(x; 𝜃) –Κ–Α–Κ –Φ–Ϋ–Ψ–≥–Ψ–Φ–Β―Ä–Ϋ―É―é –Ϋ–Ψ―Ä–Φ–Α–Μ―¨–Ϋ―É―é (–≥–Α―É―¹―¹–Ψ–≤―¹–Κ–Α―è) –Ω–Μ–Ψ―²–Ϋ–Ψ―¹―²―¨
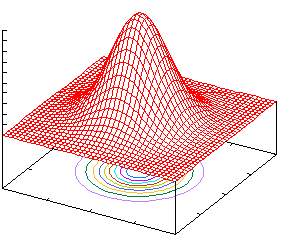
–†–Η―¹.1: ―³―É–Ϋ–Κ―Ü–Η―è –™–Α―É―¹―¹–Α
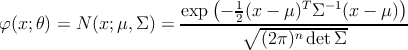
–£ ―ç―²–Ψ–Φ ―¹–Μ―É―΅–Α–Β ―Ä–Β―à–Β–Ϋ–Η–Β –Ζ–Α–¥–Α―΅–Η (1) –Ω–Ψ –Ϋ–Α―Ö–Ψ–Ε–¥–Β–Ϋ–Η―é –Ψ–Ω―²–Η–Φ–Α–Μ―¨–Ϋ―΄―Ö 𝜃j = (ΈΦj, ΈΘj) –≤―΄–≥–Μ―è–¥–Η―² ―¹–Μ–Β–¥―É―é―â–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ (j = 1,βÄΠ,k)
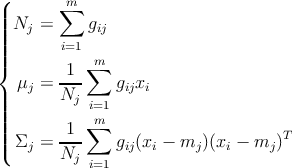
4.1 –†–Β–Α–Μ–Η–Ζ–Α―Ü–Η―è –±–Α–Ζ–Ψ–≤–Ψ–≥–Ψ EM-–Α–Μ–≥–Ψ―Ä–Η―²–Φ–Α
–£ ―ç―²–Ψ–Φ –Ω―Ä–Η–Φ–Β―Ä–Β –±―É–¥–Β–Φ –Η―¹–Κ–Α―²―¨ ―¹–Φ–Β―¹―¨ –Η–Ζ –¥–≤―É―Ö –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―² (k = 2).
–ù–Α―΅–Α–Μ―¨–Ϋ―΄–Β –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è ΈΦ1 - –Φ–Α―².–Ψ–Ε–Η–¥–Α–Ϋ–Η–Β –Ϋ–Α X, ΈΦ2 –≥–Β–Ϋ–Β―Ä–Η―Ä―É–Β―²―¹―è ―¹–Μ―É―΅–Α–Ι–Ϋ―΄–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, –Ϋ–Α―΅–Α–Μ―¨–Ϋ―΄–Β –Φ–Α―²―Ä–Η―Ü―΄ –Κ–Ψ–≤–Α―Ä–Η–Α―Ü–Η–Ι ΈΘ1 = ΈΘ1 = cov(X)
–û―²–Φ–Β―²–Η–Φ, ―΅―²–Ψ ―Ä–Β–Ζ―É–Μ―¨―²–Α―² –Ζ–Α–≤–Η―¹–Η―² –Ψ―² –Ϋ–Α―΅–Α–Μ―¨–Ϋ―΄―Ö –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Ι –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–≤, –Η –≤―΄–±―Ä–Α–Ϋ–Ϋ―΄–Ι ―¹–Ω–Ψ―¹–Ψ–± –Η–Ϋ–Η―Ü–Η–Α–Μ–Η–Ζ–Α―Ü–Η–Η ―è–≤–Μ―è–Β―²―¹―è –Ϋ–Β ―¹–Α–Φ―΄–Φ ―É–¥–Α―΅–Ϋ―΄–Φ, –≤ –¥–Α–Ϋ–Ϋ–Ψ–Φ ―¹–Μ―É―΅–Α–Β –Ψ–Ϋ –±―΄–Μ –≤―΄–±―Ä–Α–Ϋ –Η–Ζ-–Ζ–Α –Β–≥–Ψ –Ω―Ä–Ψ―¹―²–Ψ―²―΄.
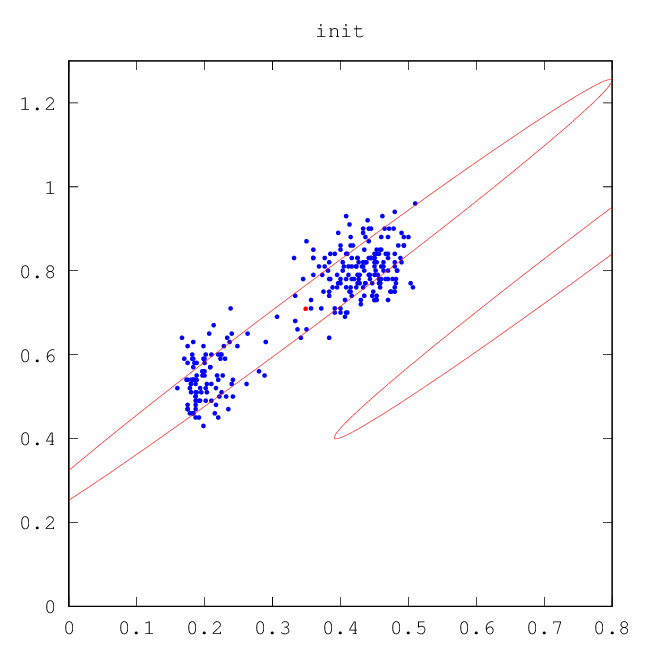
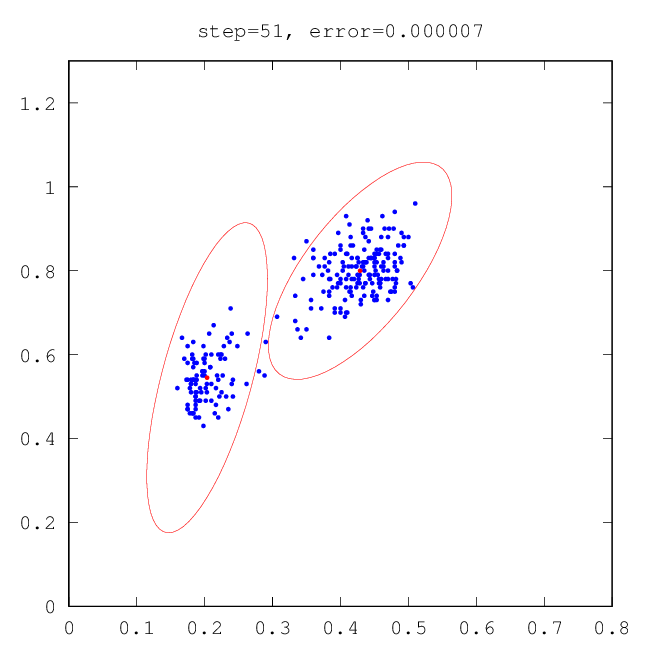
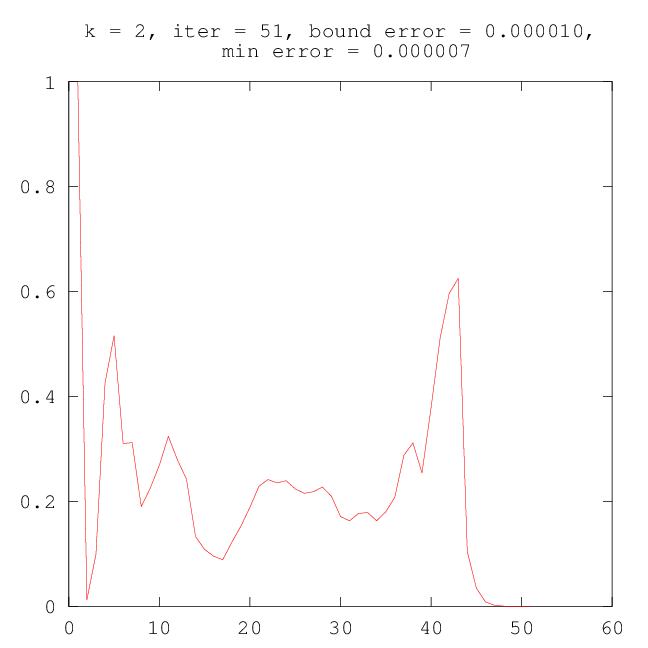
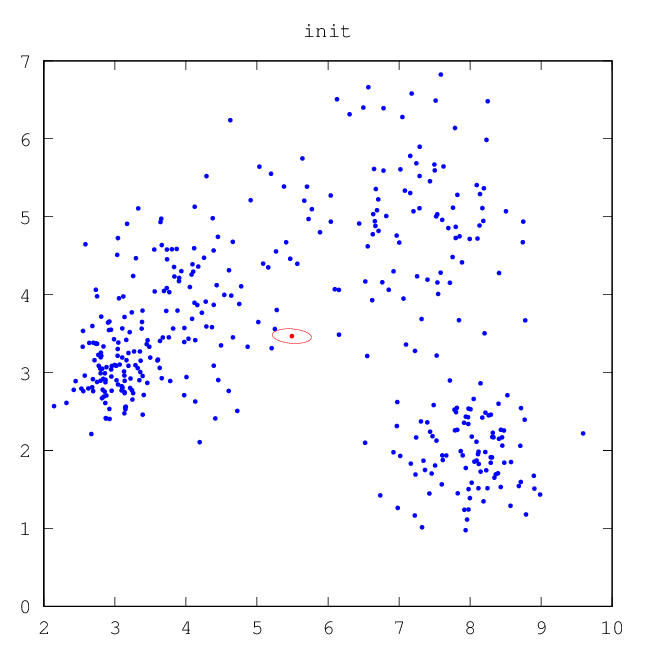
–ù–Α ―Ä–Η―¹―É–Ϋ–Κ–Α―Ö –Ϋ–Η–Ε–Β –Ω―Ä–Ψ–Η–Μ–Μ―é―¹―²―Ä–Η―Ä–Ψ–≤–Α–Ϋ–Α ―Ä–Α–±–Ψ―²–Α –ï–€-–Α–Μ–≥–Ψ―Ä–Η―²–Φ–Α, –Κ–Ψ―²–Ψ―Ä―΄–Ι –≤–Ψ―¹―¹―²–Α–Ϋ–Α–≤–Μ–Η–≤–Α–Β―² ―¹–Φ–Β―¹―¨ –Ω–Μ–Ψ―²–Ϋ–Ψ―¹―²–Β–Ι.
–†–Β–Α–Μ–Η–Ζ–Α―Ü–Η―è –≤ ―¹–Η―¹―²–Β–Φ–Β Octave [ –Ζ–¥–Β―¹―¨ ].
4.2 –†–Β–Α–Μ–Η–Ζ–Α―Ü–Η―è –Ω–Ψ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ–≥–Ψ EM-–Α–Μ–≥–Ψ―Ä–Η―²–Φ–Α
–ù–Α ―Ä–Η―¹―É–Ϋ–Κ–Α―Ö –Ϋ–Η–Ε–Β –Ω―Ä–Ψ–Η–Μ–Μ―é―¹―²―Ä–Η―Ä–Ψ–≤–Α–Ϋ–Α ―Ä–Α–±–Ψ―²–Α –Ω–Ψ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ–≥–Ψ –ï–€-–Α–Μ–≥–Ψ―Ä–Η―²–Φ–Α, –Κ–Ψ―²–Ψ―Ä―΄–Ι –≤–Ψ―¹―¹―²–Α–Ϋ–Α–≤–Μ–Η–≤–Α–Β―² ―¹–Φ–Β―¹―¨ –Ω–Μ–Ψ―²–Ϋ–Ψ―¹―²–Β–Ι.
 |
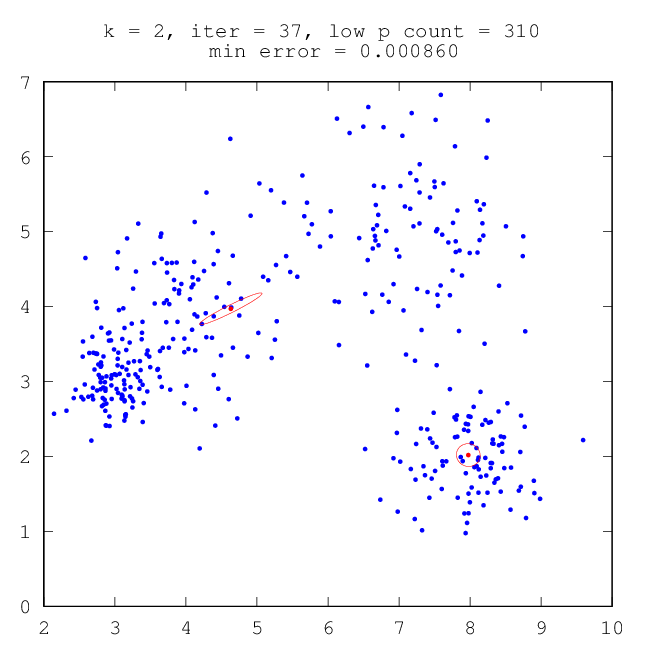 |
| –†–Η―¹.7: –Ϋ–Α―΅–Α–Μ―¨–Ϋ–Ψ–Β ―¹–Ψ―¹―²–Ψ―è–Ϋ–Η–Β | –†–Η―¹.8: –Ω―Ä–Ψ–Φ–Β–Ε―É―²–Ψ―΅–Ϋ―΄–Ι ―Ä–Β–Ζ―É–Μ―¨―²–Α―² ―Ä–Α–±–Ψ―²―΄ –ï–€ (–¥–≤–Β –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²―΄) |
| | |
 |
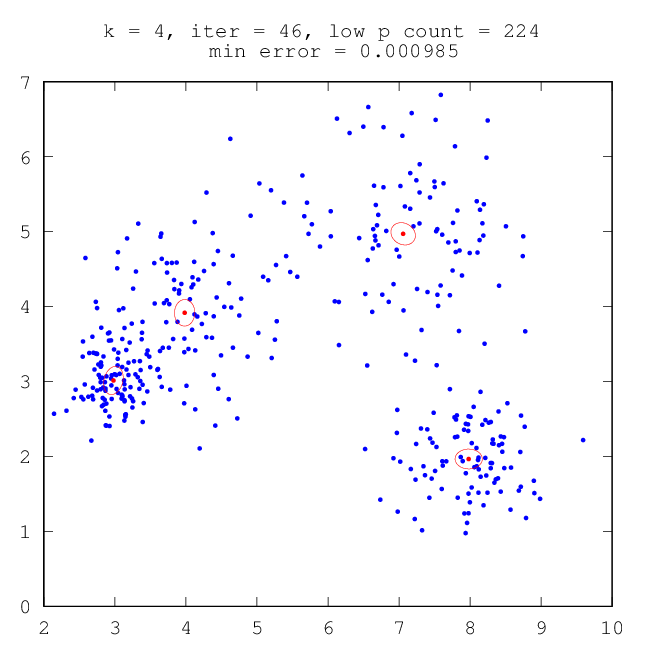 |
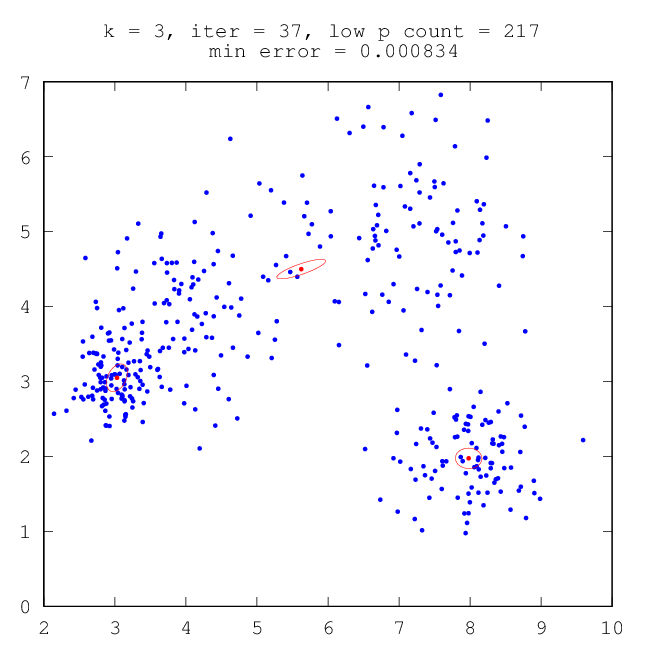
| –†–Η―¹.9: –Ω―Ä–Ψ–Φ–Β–Ε―É―²–Ψ―΅–Ϋ―΄–Ι ―Ä–Β–Ζ―É–Μ―¨―²–Α―² ―Ä–Α–±–Ψ―²―΄ –ï–€ (―²―Ä–Η –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²―΄) | –†–Η―¹.10: –Ψ–Κ–Ψ–Ϋ―΅–Α―²–Β–Μ―¨–Ϋ―΄–Ι ―Ä–Β–Ζ―É–Μ―¨―²–Α―² ―Ä–Α–±–Ψ―²―΄ –ï–€ (―΅–Β―²―΄―Ä–Β –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²―΄) |
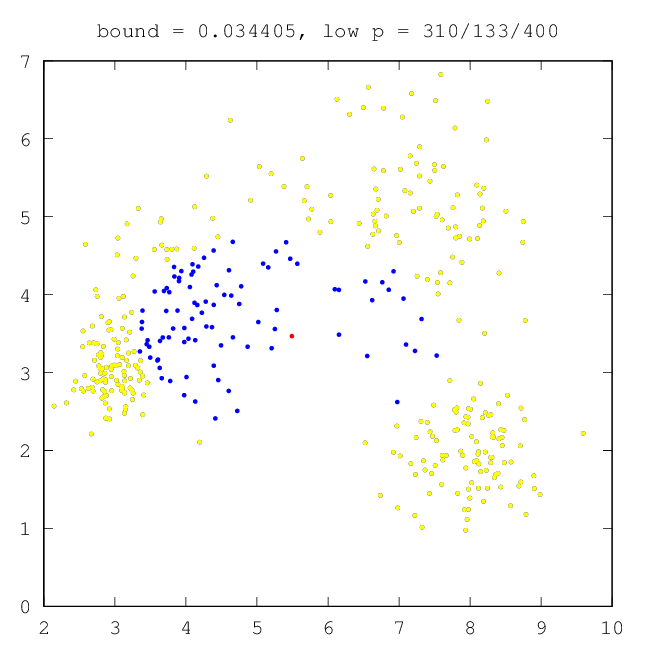
–ù–Α ―Ä–Η―¹―É–Ϋ–Κ–Α―Ö –Ϋ–Η–Ε–Β –Ω―Ä–Ψ–Η–Μ–Μ―é―¹―²―Ä–Η―Ä–Ψ–≤–Α–Ϋ–Ψ –Η–Ζ–Φ–Β–Ϋ–Β–Ϋ–Η–Β –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Α ―²–Ψ―΅–Β–Κ ―¹ –Ϋ–Η–Ζ–Κ–Η–Φ –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β–Φ –Ω–Μ–Ψ―²–Ϋ–Ψ―¹―²–Η (–Ψ―²–Φ–Β―΅–Β–Ϋ―΄ –Ε–Β–Μ―²―΄–Φ ―Ü–≤–Β―²–Ψ–Φ) –Ϋ–Α ―Ä–Α–Ζ–Ϋ―΄―Ö ―ç―²–Α–Ω–Α―Ö –≤―΄–Ω–Ψ–Μ–Ϋ–Β–Ϋ–Η―è –Α–Μ–≥–Ψ―Ä–Η―²–Φ–Α.
 |
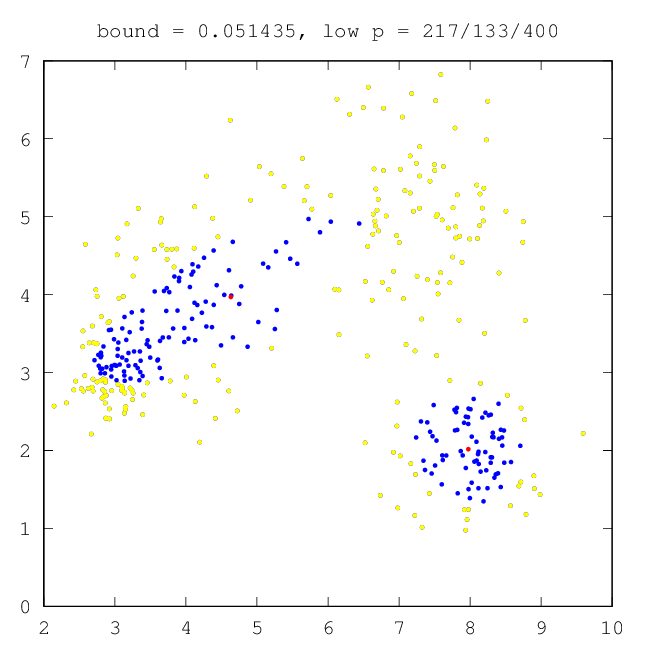 |
| –†–Η―¹.11: –Ϋ–Α―΅–Α–Μ―¨–Ϋ–Ψ–Β ―¹–Ψ―¹―²–Ψ―è–Ϋ–Η–Β | –†–Η―¹.12: –Ω―Ä–Ψ–Φ–Β–Ε―É―²–Ψ―΅–Ϋ―΄–Ι ―Ä–Β–Ζ―É–Μ―¨―²–Α―² ―Ä–Α–±–Ψ―²―΄ –ï–€ (–¥–≤–Β –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²―΄) |
| | |
 |
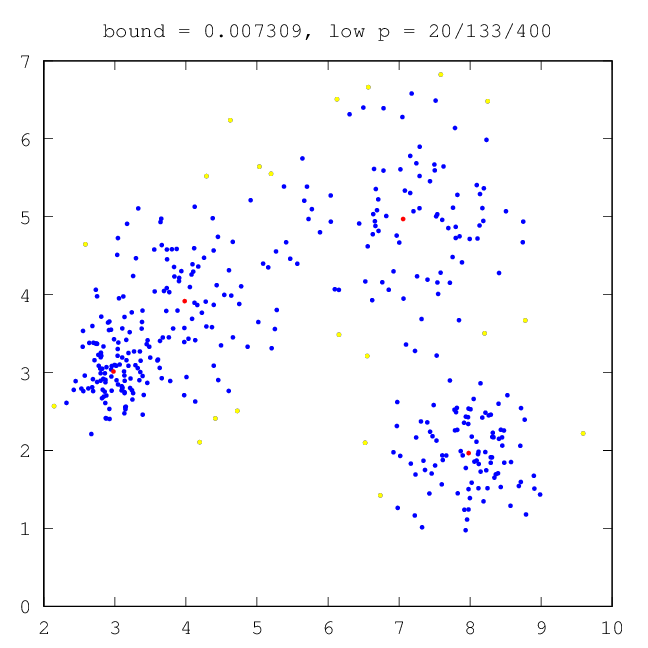 |
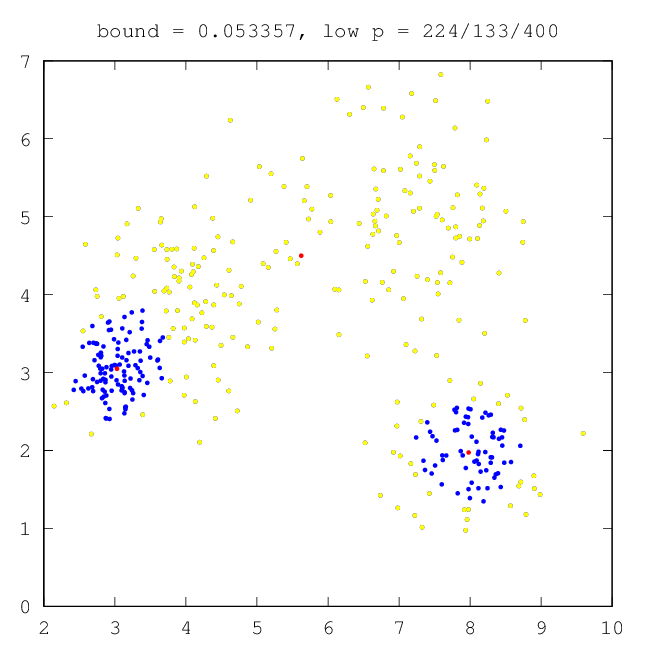
| –†–Η―¹.13: –Ω―Ä–Ψ–Φ–Β–Ε―É―²–Ψ―΅–Ϋ―΄–Ι ―Ä–Β–Ζ―É–Μ―¨―²–Α―² ―Ä–Α–±–Ψ―²―΄ –ï–€ (―²―Ä–Η –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²―΄) | –†–Η―¹.14: –Ψ–Κ–Ψ–Ϋ―΅–Α―²–Β–Μ―¨–Ϋ―΄–Ι ―Ä–Β–Ζ―É–Μ―¨―²–Α―² ―Ä–Α–±–Ψ―²―΄ –ï–€ (―΅–Β―²―΄―Ä–Β –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²―΄) |
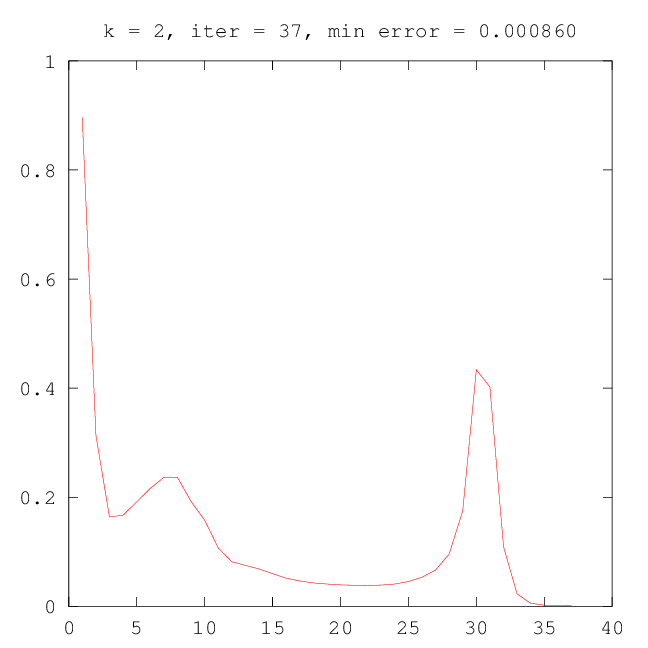
–ù–Α ―Ä–Η―¹―É–Ϋ–Κ–Α―Ö –Ϋ–Η–Ε–Β –Ω―Ä–Ψ–Η–Μ–Μ―é―¹―²―Ä–Η―Ä–Ψ–≤–Α–Ϋ–Ψ –Η–Ζ–Φ–Β–Ϋ–Β–Ϋ–Η–Β –Ω–Α―Ä–Α–Φ–Β―²―Ä–Α g –Ϋ–Α ―Ä–Α–Ζ–Ϋ―΄―Ö ―ç―²–Α–Ω–Α―Ö –≤―΄–Ω–Ψ–Μ–Ϋ–Β–Ϋ–Η―è –Α–Μ–≥–Ψ―Ä–Η―²–Φ–Α.
 |
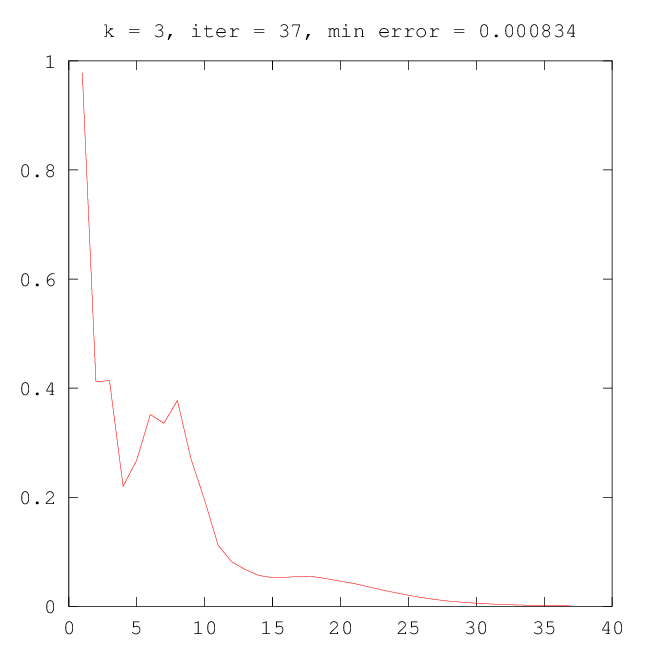 |
| –†–Η―¹.15: –Ω―Ä–Ψ–Φ–Β–Ε―É―²–Ψ―΅–Ϋ―΄–Ι ―Ä–Β–Ζ―É–Μ―¨―²–Α―² ―Ä–Α–±–Ψ―²―΄ –ï–€ (–¥–≤–Β –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²―΄) | –†–Η―¹.16: –Ω―Ä–Ψ–Φ–Β–Ε―É―²–Ψ―΅–Ϋ―΄–Ι ―Ä–Β–Ζ―É–Μ―¨―²–Α―² ―Ä–Α–±–Ψ―²―΄ –ï–€ (―²―Ä–Η –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²―΄) |
| | |
 |
|
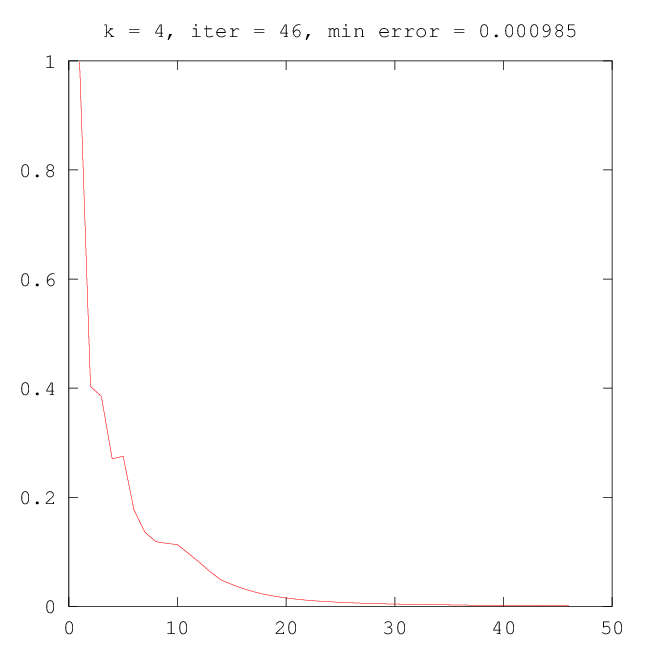
| –†–Η―¹.17: –Ω―Ä–Ψ–Φ–Β–Ε―É―²–Ψ―΅–Ϋ―΄–Ι ―Ä–Β–Ζ―É–Μ―¨―²–Α―² ―Ä–Α–±–Ψ―²―΄ –ï–€ (―΅–Β―²―΄―Ä–Β –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²―΄) | |
–†–Β–Α–Μ–Η–Ζ–Α―Ü–Η―è –≤ ―¹–Η―¹―²–Β–Φ–Β Octave [ –Ζ–¥–Β―¹―¨ ].
–Γ–Ω–Η―¹–Ψ–Κ –Μ–Η―²–Β―Ä–Α―²―É―Ä―΄
[1] –£–Ψ―Ä–Ψ–Ϋ―Ü–Ψ–≤ –ö.–£. –Γ―²–Α―²–Η―¹―²–Η―΅–Β―¹–Κ–Η–Β –Φ–Β―²–Ψ–¥―΄ –Κ–Μ–Α―¹―¹–Η―³–Η–Κ–Α―Ü–Η–Η βÄ™ http://shad.yandex.ru/lectures/machine_learning.xml