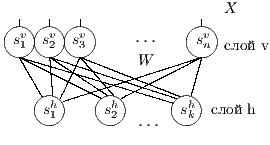
–ê—Å—Å–æ—Ü–∏–∞—Ç–∏–≤–Ω–∞—è –ø–∞–º—è—Ç—å –Ω–∞ –æ—Å–Ω–æ–≤–µ –æ–≥—Ä–∞–Ω–∏—á–µ–Ω–Ω–æ–π –º–∞—à–∏–Ω—ã –ë–æ–ª—å—Ü–º–∞–Ω–∞ (RBM).
–ï.–°.–ë–æ—Ä–∏—Å–æ–≤
–ø–æ–Ω–µ–¥–µ–ª—å–Ω–∏–∫, 26 –º–∞—è 2014 –≥.
–í —ç—Ç–æ–π —Å—Ç–∞—Ç—å–µ –º—ã –ø–æ–≥–æ–≤–æ—Ä–∏–º –æ –º–æ–¥–µ–ª–∏, –∫–æ—Ç–æ—Ä–∞—è –Ω–æ—Å–∏—Ç –Ω–∞–∑–≤–∞–Ω–∏–µ –æ–≥—Ä–∞–Ω–∏—á–µ–Ω–Ω–∞—è –º–∞—à–∏–Ω–∞ –ë–æ–ª—å—Ü–º–∞–Ω–∞ (Restricted Boltzmann Machines, RBM ).
1 –í–≤–µ–¥–µ–Ω–∏–µ
RBM [2] –ø—Ä–µ–¥—Å—Ç–∞–≤–ª—è–µ—Ç —Å–æ–±–æ–π –º–æ–¥–∏—Ñ–∏–∫–∞—Ü–∏—é –∏—Å–∫—É—Å—Å—Ç–≤–µ–Ω–Ω–æ–π –Ω–µ–π—Ä–æ–Ω–Ω–æ–π —Å–µ—Ç–∏ –º–∞—à–∏–Ω–∞ –ë–æ–ª—å—Ü–º–∞–Ω–∞, –Ω–µ–π—Ä–æ–Ω—ã –±—ã–ª–∏ —Ä–∞–∑–¥–µ–ª–µ–Ω—ã –Ω–∞ –¥–≤–µ –≥—Ä—É–ø–ø—ã, –∏ —É–±—Ä–∞–Ω—ã –Ω–µ–∫–æ—Ç–æ—Ä—ã–µ —Å–≤—è–∑–∏, —Ç–∞–∫–∏–º –æ–±—Ä–∞–∑–æ–º –±—ã–ª –æ–±—Ä–∞–∑–æ–≤–∞–Ω –≤—Ç–æ—Ä–æ–π (—Å–∫—Ä—ã—Ç—ã–π) —Å–ª–æ–π.
2 –ê–ª–≥–æ—Ä–∏—Ç–º —Ñ—É–Ω–∫—Ü–∏–æ–Ω–∏—Ä–æ–≤–∞–Ω–∏—è
–°–µ—Ç—å —Å–æ—Å—Ç–æ–∏—Ç –∏–∑ —Å—Ç–æ—Ö–∞—Å—Ç–∏—á–µ—Å–∫–∏—Ö –Ω–µ–π—Ä–æ–Ω–æ–≤ –ø—Ä–∏–Ω–∏–º–∞—é—â–∏—Ö –∑–Ω–∞—á–µ–Ω–∏—è $0$ –∏–ª–∏ $1$, —Ñ–æ—Ä–º—É–ª–∞ –≤–µ—Ä–æ—è—Ç–Ω–æ—Å—Ç–∏ –Ω–µ–π—Ä–æ–Ω–∞ –≤—ã–≥–ª—è–¥–∏—Ç —Å–ª–µ–¥—É—é—â–∏–º –æ–±—Ä–∞–∑–æ–º. $$ p(h=1|v,W,b_h) = \sigma (W \cdot v + b_h ) $$ –≥–¥–µ $v$ - –≤—Ö–æ–¥ –Ω–µ–π—Ä–æ–Ω–∞, $W$ - –≤–µ–∫—Ç–æ—Ä –≤–µ—Å–æ–≤, $b_h$ - —Å–¥–≤–∏–≥ –Ω–µ–π—Ä–æ–Ω–∞, $\sigma(x)$ - —ç–∫—Å–ø–æ–Ω–µ–Ω—Ü–∏–∞–ª—å–Ω—ã–π —Å–∏–≥–º–æ–∏–¥ $$ \sigma(x) = \frac{1}{1+\exp(-x)} $$ –≠—Ç–æ –±–∞–∑–æ–≤—ã–π –≤–∞—Ä–∏–∞–Ω—Ç —Å–µ—Ç–∏ –¥–ª—è –±–∏–Ω–∞—Ä–Ω—ã—Ö –≤—Ö–æ–¥–æ–≤ (Bernoulli-Bernoulli RBM), —Å—É—â–µ—Å—Ç–≤—É—é—Ç —Ç–∞–∫ –∂–µ –º–æ–¥–∏—Ñ–∏–∫–∞—Ü–∏–∏ –¥–ª—è –≤–µ—â–µ—Å—Ç–≤–µ–Ω–Ω—ã—Ö –≤—Ö–æ–¥–æ–≤ (Gaussian-Bernoulli RBM –∏ –¥—Ä.).–ê–ª–≥–æ—Ä–∏—Ç–º —Ñ—É–Ω–∫—Ü–∏–æ–Ω–∏—Ä–æ–≤–∞–Ω–∏—è –æ–≥—Ä–∞–Ω–∏—á–µ–Ω–Ω–æ–π –º–∞—à–∏–Ω—ã –ë–æ–ª—å—Ü–º–∞–Ω–∞ –≤—ã–≥–ª—è–¥–∏—Ç —Å–ª–µ–¥—É—é—â–∏–º –æ–±—Ä–∞–∑–æ–º.
- —É—Å—Ç–∞–Ω–∞–≤–ª–∏–≤–∞–µ–º –Ω–∞—á–∞–ª—å–Ω—ã–µ –∑–Ω–∞—á–µ–Ω–∏—è –≤—Ö–æ–¥–Ω–æ–≥–æ —Å–ª–æ—è v := x
- –≤—ã—á–∏—Å–ª–∏—Ç—å –≤–µ—Ä–æ—è—Ç–Ω–æ—Å—Ç–∏ ph –∏–∑–º–µ–Ω–µ–Ω–∏—è –Ω–µ–π—Ä–æ–Ω–æ–≤ –≤—Ç–æ—Ä–æ–≥–æ —Å–ª–æ—è
ph:=σ(v·W - bv) –≥–¥–µ W ‚Äì –º–∞—Ç—Ä–∏—Ü–∞ –≤–µ—Å–æ–≤, bv ‚Äì –≤–µ–∫—Ç–æ—Ä —Å–¥–≤–∏–≥–æ–≤ –ø–µ—Ä–≤–æ–≥–æ —Å–ª–æ—è, œÉ ‚Äì —Ñ—É–Ω–∫—Ü–∏—è –∞–∫—Ç–∏–≤–∞—Ü–∏–∏ (—Å–∏–≥–º–æ–∏–¥)
- сохранить старые значения входного слоя v′ := v
- –æ–ø—Ä–µ–¥–µ–ª–∏—Ç—å —Å–æ—Å—Ç–æ—è–Ω–∏–µ –≤—Ç–æ—Ä–æ–≥–æ —Å–ª–æ—è h, –ø—Ä–∏—Å–≤–æ–∏—Ç—å –Ω–µ–π—Ä–æ–Ω–∞–º —Å–æ—Å—Ç–æ—è–Ω–∏—è 0 –∏–ª–∏ 1 —Å –≤–µ—Ä–æ—è—Ç–Ω–æ—Å—Ç—è–º–∏ ph
- –≤—ã—á–∏—Å–ª–∏—Ç—å –≤–µ—Ä–æ—è—Ç–Ω–æ—Å—Ç–∏ pv –∏–∑–º–µ–Ω–µ–Ω–∏—è –Ω–µ–π—Ä–æ–Ω–æ–≤ –ø–µ—Ä–≤–æ–≥–æ —Å–ª–æ—è
pv:=σ(h·WT - bh) –≥–¥–µ W ‚Äì –º–∞—Ç—Ä–∏—Ü–∞ –≤–µ—Å–æ–≤, bh ‚Äì –≤–µ–∫—Ç–æ—Ä —Å–¥–≤–∏–≥–æ–≤ –≤—Ç–æ—Ä–æ–≥–æ —Å–ª–æ—è, œÉ ‚Äì —Ñ—É–Ω–∫—Ü–∏—è –∞–∫—Ç–∏–≤–∞—Ü–∏–∏ (—Å–∏–≥–º–æ–∏–¥)
- –æ–ø—Ä–µ–¥–µ–ª–∏—Ç—å —Å–æ—Å—Ç–æ—è–Ω–∏–µ –ø–µ—Ä–≤–æ–≥–æ —Å–ª–æ—è v, –ø—Ä–∏—Å–≤–æ–∏—Ç—å –Ω–µ–π—Ä–æ–Ω–∞–º —Å–æ—Å—Ç–æ—è–Ω–∏—è 1 —Å –≤–µ—Ä–æ—è—Ç–Ω–æ—Å—Ç—è–º–∏ pv (–∏–ª–∏ —Å–æ–æ—Ç–≤–µ—Ç—Å–≤–µ–Ω–Ω–æ 0 —Å –≤–µ—Ä–æ—è—Ç–Ω–æ—Å—Ç—è–º–∏ 1-pv)
- –µ—Å–ª–∏ v‚âÝv‚Ä≤
—Ç–æ –ø–æ–≤—Ç–æ—Ä–∏—Ç—å —Å –ø.2
–∏–Ω–∞—á–µ –ø–µ—Ä–µ–π—Ç–∏ –Ω–∞ —Å–ª–µ–¥—É—é—â–∏–π –ø—É–Ω–∫—Ç - –≤—ã–¥–∞—á–∞ —Ä–µ–∑—É–ª—å—Ç–∞—Ç–∞ v
- –∫–æ–Ω–µ—Ü —Ä–∞–±–æ—Ç—ã
3 –ú–µ—Ç–æ–¥ –æ–±—É—á–µ–Ω–∏—è
–ê–ª–≥–æ—Ä–∏—Ç–º –æ–±—É—á–µ–Ω–∏—è –æ–≥—Ä–∞–Ω–∏—á–µ–Ω–Ω–æ–π –º–∞—à–∏–Ω—ã –ë–æ–ª—å—Ü–º–∞–Ω–∞ –Ω–∞–∑—ã–≤–∞–µ—Ç—Å—è Contrastive Divergence (CD) –∏ –ø—Ä–µ–¥—Å—Ç–∞–≤–ª—è–µ—Ç —Å–æ–±–æ–π –Ω–µ–º–Ω–æ–≥–æ –º–æ–¥–∏—Ñ–∏—Ü–∏—Ä–æ–≤–∞–Ω–Ω—ã–π –º–µ—Ç–æ–¥ –≥—Ä–∞–¥–∏–µ–Ω—Ç–Ω–æ–≥–æ —Å–ø—É—Å–∫–∞.
–í –∫–∞—á–µ—Å—Ç–≤–µ —Ñ—É–Ω–∫—Ü–∏–∏ –æ—Ü–µ–Ω–∫–∏, –∫–æ—Ç–æ—Ä—É—é –Ω–µ–æ–±—Ö–æ–¥–∏–º–æ –æ–ø—Ç–∏–º–∏–∑–∏—Ä–æ–≤–∞—Ç—å, –∏—Å–ø–æ–ª—å–∑—É–µ—Ç—Å—è —Ñ—É–Ω–∫—Ü–∏—è –ø—Ä–∞–≤–¥–æ–ø–æ–¥–æ–±–∏—è $L$ (likehood), –±—É–¥–µ–º –∏—Å–∫–∞—Ç—å –µ—ë –º–∞–∫—Å–∏–º—É–º. –§—É–Ω–∫—Ü–∏—è –ø—Ä–∞–≤–¥–æ–ø–æ–¥–æ–±–∏—è $L$ –¥–ª—è –ø–∞—Ä–∞–º–µ—Ç—Ä–æ–≤ $(W,b_v,b_h)$ –∏ –æ–±—Ä–∞–∑–∞ $v$ –æ–ø—Ä–µ–¥–µ–ª—è–µ—Ç—Å—è –∫–∞–∫ –≤–µ—Ä–æ—è—Ç–Ω–æ—Å—Ç–∏ –≤–∏–¥–∏–º–æ–≥–æ —Å–ª–æ—è $v$ –ø—Ä–∏ –¥–∞–Ω–Ω—ã—Ö –ø–∞—Ä–∞–º–µ—Ç—Ä–∞—Ö. $$ L(W,b_v,b_h|v) = p(v|W,b_v,b_h) $$ –î–ª—è —É–¥–æ–±—Å—Ç–≤–∞ –≤—ã—á–∏—Å–ª–µ–Ω–∏–π –±—É–¥–µ–º –∏—Å–ø–æ–ª—å–∑–æ–≤–∞—Ç—å –ª–æ–≥–∞—Ä–∏—Ñ–º $$ \ln L(W,b_v,b_h|v) = \ln \sum\limits_h \exp (-E(v,h)) - \ln \sum\limits_{v,h} \exp (-E(v,h)) $$ –≥–¥–µ $E$ - —ç–Ω–µ—Ä–≥–∏—è —Å–µ—Ç–∏ $$ E(v,h) = - ( b_v \cdot v + b_h \cdot h + v\cdot h\cdot W ) $$ –ì—Ä–∞–¥–∏–µ–Ω—Ç —Ñ—É–Ω–∫—Ü–∏–∏ –æ—Ü–µ–Ω–∫–∏ –≤—ã–≥–ª—è–¥–∏—Ç —Å–ª–µ–¥—É—é—â–∏–º –æ–±—Ä–∞–∑–æ–º \begin{equation} \left\{\begin{array}{ r c l } \frac{\partial \ln L(W,b_v,b_h|v) }{\partial W} = \nabla W & = & (v\cdot h)_{data} - (v\cdot h)_{model} \\ \frac{\partial \ln L(W,b_v,b_h|v) }{\partial b_v} = \nabla b_v & = & (v)_{data} - (v)_{model} \\ \frac{\partial \ln L(W,b_v,b_h|v) }{\partial b_h} = \nabla b_h & = & (h)_{data} - (h)_{model} \end{array} \right. \label{eq:grad} \end{equation} –∑–¥–µ—Å—å $(\cdot)_{data}$ - –∑–Ω–∞—á–µ–Ω–∏–µ —Å–ª–æ—ë–≤ –≤ –Ω–∞—á–∞–ª—å–Ω–æ–º —Å–æ—Å—Ç–æ—è–Ω–∏–∏ —Å–µ—Ç–∏, $(\cdot)_{model}$ - –º–∞—Ç.–æ–∂–∏–¥–∞–Ω–∏–µ —Å–æ—Å—Ç–æ—è–Ω–∏—è —Å–ª–æ—ë–≤. –ú–∞—Ç.–æ–∂–∏–¥–∞–Ω–∏–µ —Å–æ—Å—Ç–æ—è–Ω–∏—è —Å–ª–æ—ë–≤ $(\cdot)_{model}$ –≤—ã—á–∏—Å–ª—è–µ—Ç—Å—è –ø—É—Ç—ë–º —Ç.–Ω. —Å—ç–º–ø–ª–∏—Ä–æ–≤–∞–Ω–∏—è, —Ç.–µ. $(\cdot)_{model}$ —ç—Ç–æ —Å—Ç–æ—è–Ω–∏–µ —Å–ª–æ—ë–≤ –ø–æ—Å–ª–µ –Ω–µ—Å–∫–æ–ª—å–∫–∏—Ö –∏—Ç–µ—Ä–∞—Ü–∏–π —Å–µ—Ç–∏, –Ω–∞ –ø—Ä–∞–∫—Ç–∏–∫–µ (–¥–ª—è —Ç–æ–≥–æ, —á—Ç–æ –±—ã –∞–ª–≥–æ—Ä–∏—Ç–º —Ä–∞–±–æ—Ç–∞–ª) –±—ã–≤–∞–µ—Ç –¥–æ—Å—Ç–∞—Ç–æ—á–Ω–æ –æ–¥–Ω–æ–≥–æ —à–∞–≥–∞ —Å—ç–º–ø–ª–∏—Ä–æ–≤–∞–Ω–∏—è (–æ–¥–Ω–æ–π –∏—Ç–µ—Ä–∞—Ü–∏–π —Å–µ—Ç–∏). –í–µ—Å–∞ –∏–∑–º–µ–Ω—è—é—Ç—Å—è —Å–ª–µ–¥—É—é—â–∏–º –æ–±—Ä–∞–∑–æ–º. \begin{equation} \left\{\begin{array}{ r c l } W & := & \varepsilon \cdot ( \nabla W + \mu \cdot \Delta W ) \\ b_v & := & \varepsilon \cdot ( \nabla b_v + \mu \cdot \Delta b_v ) \\ b_h & := & \varepsilon \cdot ( \nabla b_h + \mu \cdot \Delta b_h ) \end{array} \right. \label{eq:wgt} \end{equation} –≥–¥–µ $\mu$ - –ø–∞—Ä–∞–º–µ—Ç—Ä –º–æ–º–µ–Ω—Ç–∞, $\varepsilon $ - —Å–∫–æ—Ä–æ—Å—Ç—å –æ–±—É—á–µ–Ω–∏—è, $\Delta W,\Delta b_v,\Delta b_h$ - –∏–∑–º–µ–Ω–µ–Ω–∏–µ –ø–∞—Ä–∞–º–µ—Ç—Ä–æ–≤ –Ω–∞ –ø—Ä–µ–¥—ã–¥—É—â–µ–º —à–∞–≥–µ. –í –∫–∞—á–µ—Å—Ç–≤–µ –∫—Ä–∏—Ç–µ—Ä–∏—è –æ—Å—Ç–∞–Ω–æ–≤–∫–∏ –æ–±—É—á–µ–Ω–∏—è –±—É–¥–µ–º –∏—Å–ø–æ–ª—å–∑–æ–≤–∞—Ç—å —Å—Ä–µ–¥–Ω–µ–∫–≤–∞–¥—Ä–∞—Ç–∏—á–Ω—É—é –æ—à–∏–±–∫—É –º–µ–∂–¥—É –≤—Ö–æ–¥–æ–º —Å–µ—Ç–∏ –∏ –µ—ë –≤—ã—Ö–æ–¥–æ–º - $E(v_0,v_k)$, –∑–Ω–∞—á–µ–Ω–∏–µ –æ—à–∏–±–∫–∏ –¥–æ–ª–∂–Ω–æ —É–º–µ–Ω—å—à–∏—Ç—å—Å—è –¥–æ —É—Å—Ç–∞–Ω–æ–≤–ª–µ–Ω–Ω–æ–≥–æ –ø–æ—Ä–æ–≥–∞ $E_{min}$. –ê–ª–≥–æ—Ä–∏—Ç–º –æ–±—É—á–µ–Ω–∏—è –≤—ã–≥–ª—è–¥–∏—Ç —Å–ª–µ–¥—É—é—â–∏–º –æ–±—Ä–∞–∑–æ–º.
- –∏–Ω–∏—Ü–∏–∞–ª–∏–∑–∏—Ä–æ–≤–∞—Ç—å (–Ω—É–ª—è–º–∏) –º–∞—Ç—Ä–∏—Ü—É –≤–µ—Å–æ–≤ W –∏ –≤–µ–∫—Ç–æ—Ä—ã —Å–¥–≤–∏–≥–æ–≤ bv, bh
- –≤—ã–±—Ä–∞—Ç—å —Å–ª—É—á–∞–π–Ω–æ–µ –ø–∞–∫–µ—Ç –∏–∑ –≤—Å–µ–≥–æ –Ω–∞–±–æ—Ä–∞ —É—á–µ–±–Ω—ã—Ö –ø—Ä–∏–º–µ—Ä–æ–≤ (mini-batch) X
- –¥–ª—è –≤—Å–µ—Ö –ø—Ä–∏–º–µ—Ä–æ–≤ –ø–∞–∫–µ—Ç–∞: –ø—Ä–∏—Å–≤–æ–∏—Ç—å –Ω–∞—á–∞–ª—å–Ω–æ–µ –∑–Ω–∞—á–µ–Ω–∏–µ –ø–µ—Ä–≤–æ–º—É —Å–ª–æ—é v := x
- выполнить k циклов сети, определить начальные и конечные состояния слоёв v0, h0, vk, hk (где k – параметр)
- –≤—ã—á–∏—Å–ª–∏—Ç—å –≥—Ä–∞–¥–∏–µ–Ω—Ç –ø–æ (\ref{eq:grad}) –∏ —Å–∫–æ—Ä—Ä–µ–∫—Ç–∏—Ä–æ–≤–∞—Ç—å –≤–µ—Å–∞ –ø–æ (\ref{eq:wgt})
- –≤—ã—á–∏—Å–ª–∏—Ç—å —Å—Ä–µ–¥–Ω–µ–∫–≤–∞–¥—Ä–∞—Ç–∏—á–Ω—É—é –æ—à–∏–±–∫—É —Å–µ—Ç–∏ E
- –µ—Å–ª–∏
$E < E_{min}$
—Ç–æ –ø–µ—Ä–µ—Ö–æ–¥ –ø.8
–∏–Ω–∞—á–µ –ø–µ—Ä–µ—Ö–æ–¥ –ø.2 - –∫–æ–Ω–µ—Ü —Ä–∞–±–æ—Ç—ã
4 –Ý–µ–∞–ª–∏–∑–∞—Ü–∏—è –∞—Å—Å–æ—Ü–∏–∞—Ç–∏–≤–Ω–æ–π –ø–∞–º—è—Ç–∏
–ó–¥–µ—Å—å –ø—Ä–µ–¥—Å—Ç–∞–≤–ª–µ–Ω–∞ —Ä–µ–∞–ª–∏–∑–∞—Ü–∏—è, –æ–ø–∏—Å–∞–Ω–Ω–æ–π –≤—ã—à–µ –º–æ–¥–µ–ª–∏. –í –Ω–∞—á–∞–ª–µ –≤ –ø–∞–º—è—Ç—å "–∑–∞–ø–∏—Å—ã–≤–∞—é—Ç—Å—è" –Ω–µ—Å–∫–æ–ª—å–∫–æ —Ä–∞–∑–Ω—ã—Ö –∫–∞—Ä—Ç–∏–Ω–æ–∫. –î–∞–ª–µ–µ - –ø–∞–º—è—Ç–∏ –ø—Ä–µ–¥—ä—è–≤–ª—è—é—Ç—Å—è –¥—Ä—É–≥–∏–µ, –ø–æ—Ö–æ–∂–∏–µ –∫–∞—Ä—Ç–∏–Ω–∫–∏, –ø–æ –∫–æ—Ç–æ—Ä—ã–º –≤–æ—Å—Å—Ç–∞–Ω–∞–≤–ª–∏–≤–∞—é—Ç—Å—è –æ—Ä–∏–≥–∏–Ω–∞–ª—ã.
—É—á–µ–±–Ω—ã–π –Ω–∞–±–æ—Ä


—Ä–µ–∑—É–ª—å—Ç–∞—Ç —Ä–∞–±–æ—Ç—ã
| –≤—Ö–æ–¥: |  |
 |
 |
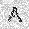 |
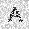 |
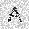 |
 |
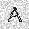 |
 |
 |
 |
 |
 |
 |
 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
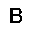 |
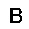 |
| –≤—Ö–æ–¥: | 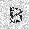 |
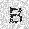 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
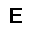 |
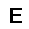 |
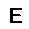 |
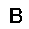 |
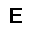 |
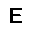 |
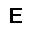 |
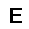 |
 |
| –≤—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
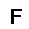 |
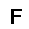 |
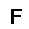 |
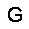 |
 |
 |
 |
 |
 |
| –≤—Ö–æ–¥: |  |
 |
 |
 |
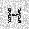 |
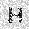 |
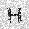 |
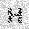 |
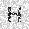 |
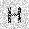 |
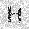 |
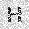 |
 |
 |
 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
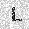 |
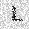 |
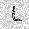 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
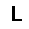 |
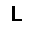 |
| –≤—Ö–æ–¥: | 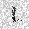 |
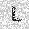 |
 |
 |
 |
 |
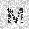 |
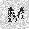 |
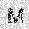 |
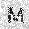 |
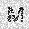 |
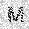 |
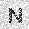 |
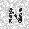 |
 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—Ö–æ–¥: | 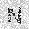 |
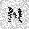 |
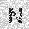 |
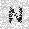 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—Ö–æ–¥: |  |
 |
 |
 |
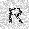 |
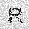 |
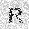 |
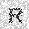 |
 |
 |
 |
 |
 |
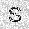 |
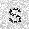 |
| –≤—ã—Ö–æ–¥: | 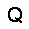 |
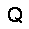 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—Ö–æ–¥: |  |
 |
 |
 |
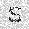 |
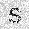 |
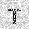 |
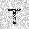 |
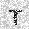 |
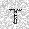 |
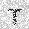 |
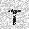 |
 |
 |
 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—Ö–æ–¥: |  |
 |
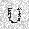 |
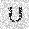 |
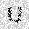 |
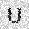 |
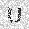 |
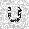 |
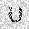 |
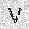 |
 |
 |
 |
 |
 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—Ö–æ–¥: | 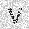 |
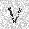 |
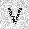 |
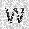 |
 |
 |
 |
 |
 |
 |
 |
 |
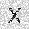 |
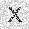 |
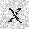 |
| –≤—ã—Ö–æ–¥: | 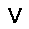 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
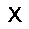 |
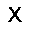 |
| –≤—Ö–æ–¥: | 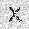 |
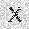 |
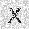 |
 |
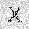 |
 |
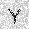 |
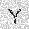 |
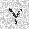 |
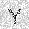 |
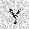 |
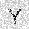 |
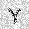 |
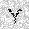 |
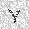 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| –≤—Ö–æ–¥: |  |
 |
 |
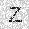 |
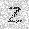 |
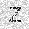 |
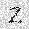 |
 |
 |
| –≤—ã—Ö–æ–¥: |  |
 |
 |
 |
 |
 |
 |
 |
 |
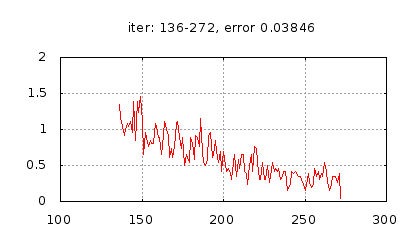
–∏—Å—Ç–æ—Ä–∏—è –∏–∑–º–µ–Ω–µ–Ω–∏—è –æ—à–∏–±–∫–∏ –æ–±—É—á–µ–Ω–∏—è
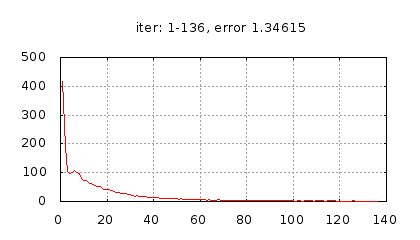
–∫–∞—Ä—Ç–∞ –≤–µ—Å–æ–≤
–ø–æ –∫–æ–ª–∏—á–µ—Å—Ç–≤—É –Ω–µ–π—Ä–æ–Ω–æ–≤ –≤—Ç–æ—Ä–æ–≥–æ (hidden) —Å–ª–æ—è












































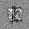



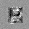


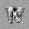















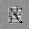















































































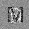
































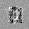













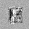









































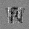




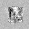












































–°–ø–∏—Å–æ–∫ –ª–∏—Ç–µ—Ä–∞—Ç—É—Ä—ã
[1] J.J.Hopfield Neural Networks and Physical Systems with Emergent Collective Computational Abilities // in Proc. National Academy of Sciencies, USA 79, 1982, pp. 2554-2558.
[2] Ackley, D. H., Hinton, G. E., and Sejnowski, T. J. A learning algorithm for Boltzmann machines. // Cognitive Science, 1985, vol.9, pp. 147–169.
[3] Restricted Boltzmann Machines (RBM) – http://deeplearning.net/tutorial/rbm.html
[4] –ü–∞–≤–µ–ª –ù–µ—Å—Ç–µ—Ä–æ–≤ –Ý–µ–∞–ª–∏–∑–∞—Ü–∏—è Restricted Boltzmann machine –Ω–∞ c# ‚Äì http://habrahabr.ru/post/159909
[5] –ï.–°.–ë–æ—Ä–∏—Å–æ–≤ –û –º–µ—Ç–æ–¥–∞—Ö –æ–±—É—á–µ–Ω–∏—è –º–Ω–æ–≥–æ—Å–ª–æ–π–Ω—ã—Ö –Ω–µ–π—Ä–æ–Ω–Ω—ã—Ö —Å–µ—Ç–µ–π –ø—Ä—è–º–æ–≥–æ —Ä–∞—Å–ø—Ä–æ—Å—Ç—Ä–∞–Ω–µ–Ω–∏—è. –ß–∞—Å—Ç—å 2: –ì—Ä–∞–¥–∏–µ–Ω—Ç–Ω—ã–µ –º–µ—Ç–æ–¥—ã –ø–µ—Ä–≤–æ–≥–æ –ø–æ—Ä—è–¥–∫–∞. -- http://mechanoid.kiev.ua/neural-net-backprop2.html
[6] Subha Manoharan Gaussian Discrete Restricted Boltzmann Machine: Theory and its applications