Задача сглаживания колебаний.
Метод скользящего среднего
и фильтр Калмана

Евгений Борисов

пятница, 21 июля 2017 г.

В статье описаны методы сглаживания колебаний в последовательностях.

1. Введение

Задача сглаживания колебаний возникает когда надо выявить основное направление изменения сильно осцилирующей последовательности. Это могут быть показания датчика уровня топлива в автомобиле или биржевые сводки. Задачу можно рассматривать как восстановление некоторой последовательности $r$ на которую был наложен шум. Различные варианты решения этой задачи мы рассмотрим далее.

2. Скользящее среднее

Начнём с простого скользящего среднего - SMA (Simple Moving Average)[1]. Для вычисления текущего значения фильтра $r_i$ мы просто усредняем предыдущие $s$ элементов последовательности, соответственно фильтр начинает работать с элемента последовательности $s$. $$ r_i = \frac{1}{s}\cdot\sum_{j=1}^s y_{(i-j)}\ ; \ i > s $$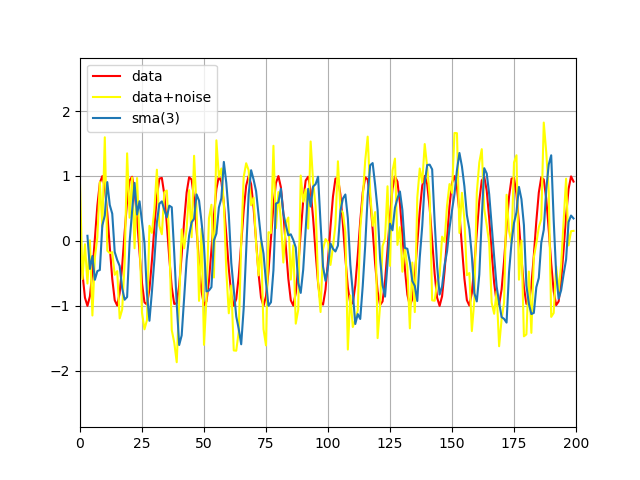

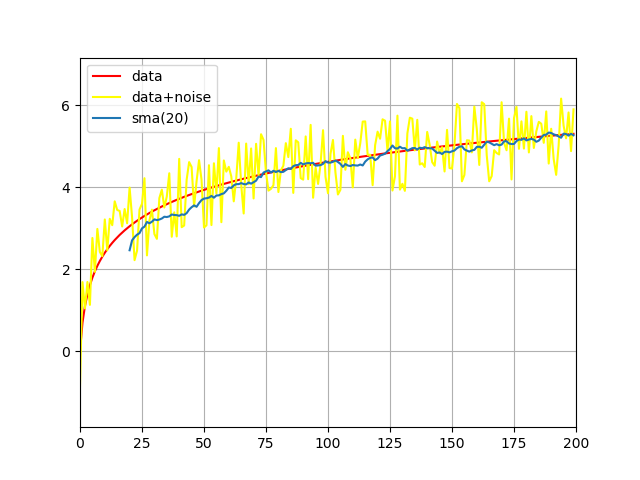
Рис 1: фильтрация с помощью метода SMA

3. Взвешенное скользящее среднее

Взвешенное скользящее среднее - WMA (Weighted Moving Average)[1], этот метод похож на предыдущий (SMA), его особенность в том, что он учитывает последовательность истории для усреднения. Это происходит путём домножения предыдущих $s$ элементов на коэффициенты-веса от $1$ до $1/s$, самый "старый" элемент имеет наибольший вес ( т.е. $1$ ). Как и в случае с SMA, фильтр начинает работать с элемента последовательности $s$. $$ r_i = \frac{2}{s\cdot(s+1)}\cdot \sum_{j=1}^s j \cdot y_{(i-j)} \ ; \ i > s $$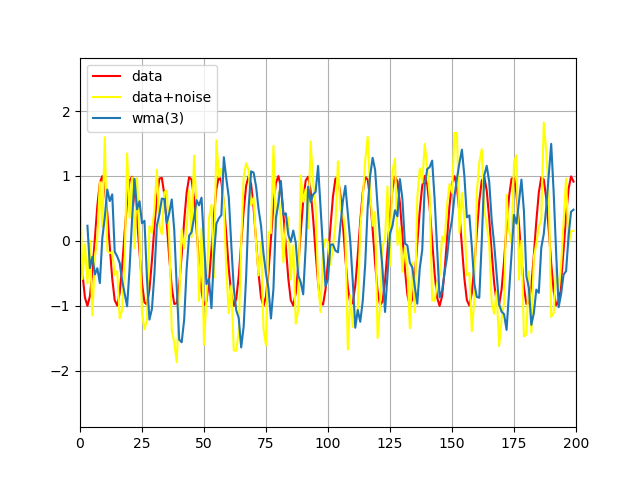

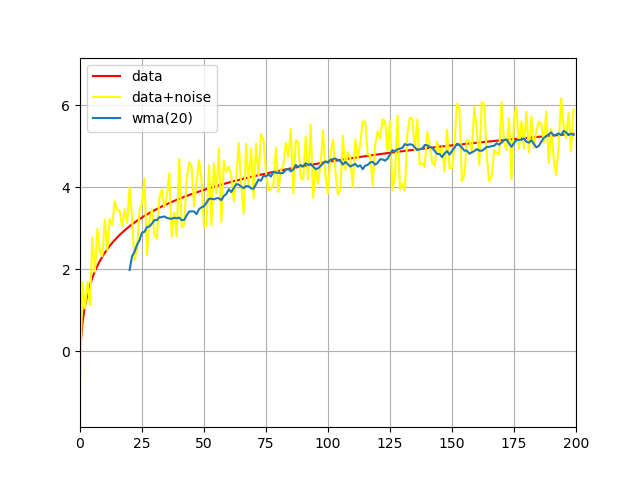
Рис 2: фильтрация с помощью метода WMA

4. Экспоненциальное скользящее среднее

Экспоненциальное скользящее среднее - EMA (Exponential Moving Average)[2]. Этот метод не требует длительной инициализации как WMA и выдаёт результат сразу. $$r_{i+1} = r_i + \frac{2}{s+1} \cdot ( y_i - r_i ) $$ $$ r_1 = y_1 $$ $$ s = const $$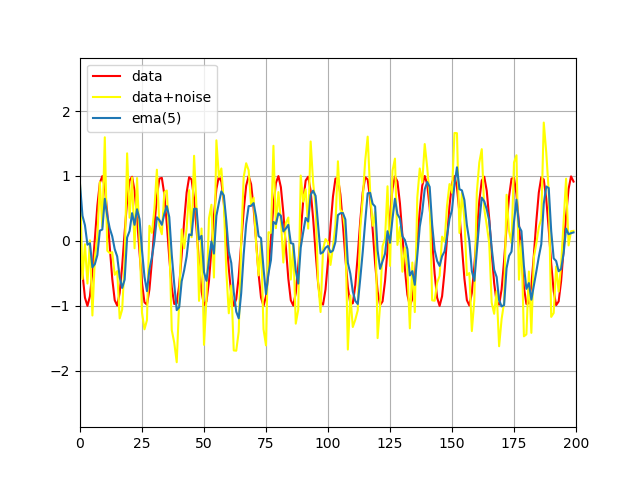

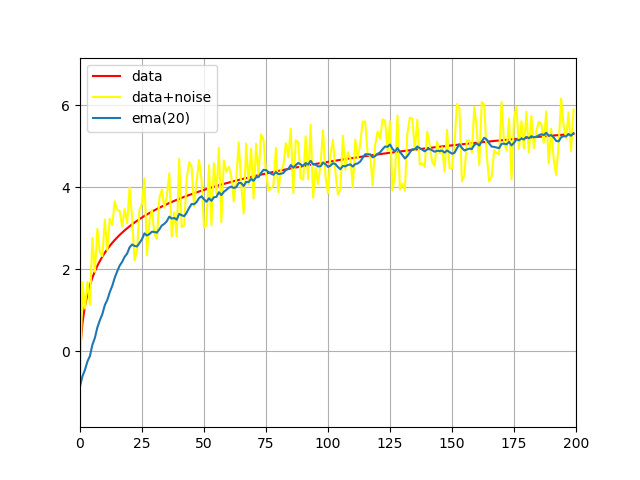
Рис 3: фильтрация с помощью метода EMA

5. Экспоненциально взвешенное скользящее среднее

Экспоненциально взвешенное скользящее среднее - EWMA (Exponentially Weighted Moving Average) или фильтр Брауна [3]. $$r_i = p\cdot y_i + (1-p)\cdot r_{i-1} $$ $$ r_1 = y_1 $$ где $0 < p < 1 $ - сглаживающая константа.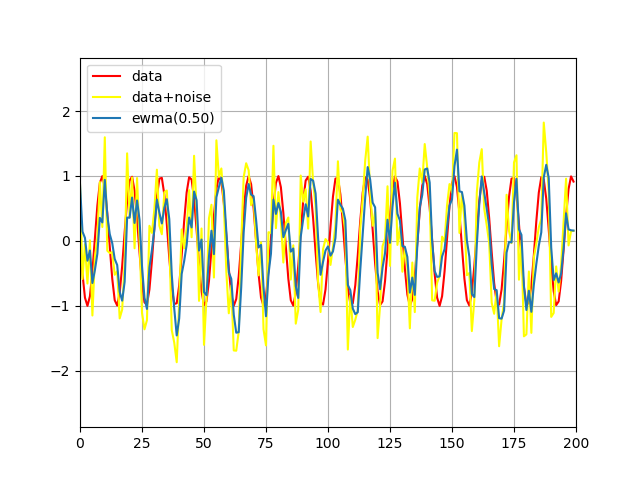

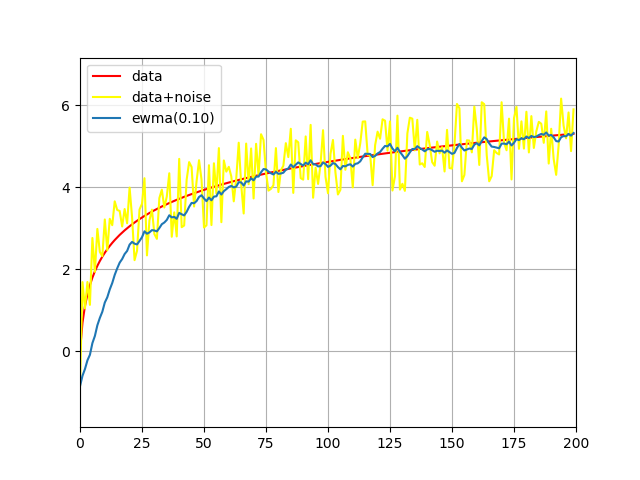
Рис 4: фильтрация с помощью метода EWMA

6. Фильтр Калмана

Фильтр Калмана [4] широко используется для фильтрации шума в различных динамических системах. Рассмотрим динамическую систему с вектором состояния $x$. $$x = F\cdot x + w(Q)$$ где $F$ - матрица переходов (transition matrix),
$w(Q)$ - случайный процесс (шум) с нулевым мат.ожиданием и матрицей ковариаций $Q$.

Будем наблюдать переходы состояний системы с известной погрешностью измерений в каждый момент времени. Фильтрация шума с помощью метода Калмана состоит из двух шагов - экстраполяция и коррекция, выглядит это следующим образом.

Зададим параметры системы.

$Q$ - матрицей ковариаций шума (process noise covariance )
$H$ - матрица наблюдения (measurement)
$R$ - ковариация шума наблюдения (measurement noise covariance)
$P = Q$ - начальное значение ковариационной матрицы для вектора состояния
$z(t)$ - наблюдаемое состояние системы
$x = z(0)$ - начальное значение оценки состояния системы

Для каждого наблюдения $z$ будем вычислять отфильтрованное состояние $x$
и для этого выполняем следующие шаги.

шаг 1: экстраполяция
1. экстраполяция (предсказание) состояния системы $$x = F\cdot x$$
2. вычисляем ковариационную матрицу для экстраполированного вектора состояния $$P = F\cdot P\cdot F^T + Q$$
шаг 2: коррекция
1. вычисляем вектор ошибки, отклонение наблюдения от ожидаемого состояния $$y = z - H \cdot x $$
2. вычисляем ковариационную матрицу для вектора отклонения (вектора ошибки) $$S = H \cdot P \cdot H^T + R$$
3. вычисляем коэффициенты усиления Калмана $$K = P\cdot H \cdot H^T \cdot S^{-1}$$
4. коррекция оценки вектора состояния $$x = x + K \cdot y$$
5. корректируем ковариационную матрицу оценки вектора состояния системы $$P = (I - K\cdot H)\cdot P$$

Далее рассмотрим пример. Сгенерируем последовательность точек $(x_1,x_2)$ на плоскости и наложим на эти данные шум. Результаты работы фильтра на рис.5.

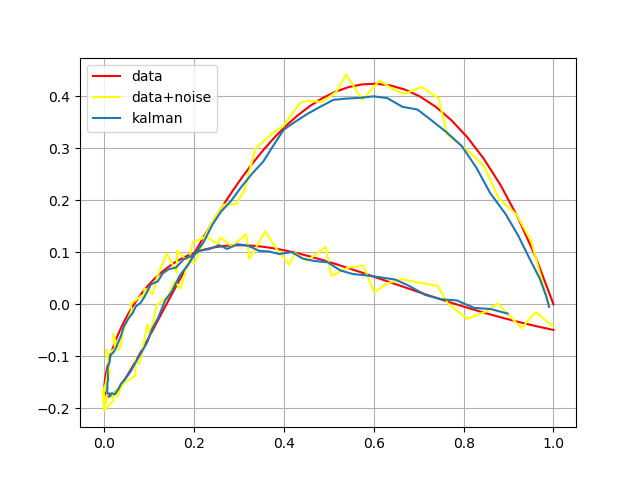
Рис 5: фильтрация с помощью метода Калмана

7. Реализация

Текст реализации методов скользящего среднего на языке python можно скачать [здесь].

Текст реализации фильтра Калмана на языке python можно скачать [здесь].

Литература

Wikipedia: Скользящая средняя - http://ru.wikipedia.org/wiki/Скользящая_средняя
Учебник Форекс: Эспоненциальное скользящее среднее. http://enc.fxeuroclub.ru/107/
Brown R.G., Meyer R.F. The fundamental theorum of exponential smoothing. Oper. Res. - 1961. - Vol.9. - N5.
Wikipedia: Фильтр Калмана - http://ru.wikipedia.org/wiki/Фильтр_Калмана

Задача сглаживания колебаний. Метод скользящего среднего и фильтр Калмана