
–Ď–į–Ļ–Ķ—Ā–ĺ–≤—Ā–ļ–ł–Ļ –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—ā–ĺ—Ä
–ē–≤–≥–Ķ–Ĺ–ł–Ļ –Ď–ĺ—Ä–ł—Ā–ĺ–≤ –≤—ā–ĺ—Ä–Ĺ–ł–ļ, 3 –ī–Ķ–ļ–į–Ī—Ä—Ź 2013 –≥.–í —ć—ā–ĺ–Ļ —Ā—ā–į—ā—Ć–Ķ –ľ—č —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ļ –ľ–Ķ—ā–ĺ–ī, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –Ī–į–Ļ–Ķ—Ā–ĺ–≤—Ā–ļ–ł–Ļ –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—ā–ĺ—Ä.
1 –í–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ
–Ď–į–Ļ–Ķ—Ā–ĺ–≤—Ā–ļ–ł–Ļ –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—ā–ĺ—Ä –ĺ—ā–Ĺ–ĺ—Ā–ł—ā—Ā—Ź –ļ –ľ–Ķ—ā–ĺ–ī–į–ľ –ľ–į—ą–ł–Ĺ–Ĺ–ĺ–≥–ĺ –ĺ–Ī—É—á–Ķ–Ĺ–ł—Ź ‚ÄĚ—Ā —É—á–ł—ā–Ķ–Ľ–Ķ–ľ‚ÄĚ, –Ĺ–ĺ –≤ –ĺ—ā–Ľ–ł—á–ł–ł –ĺ—ā –Ņ–Ķ—Ä—Ü–Ķ–Ņ—ā—Ä–ĺ–Ĺ–į –ł –ī—Ä—É–≥–ł—Ö –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č—Ö –ľ–ĺ–ī–Ķ–Ľ–Ķ–Ļ, –ĺ–Ĺ –Ĺ–Ķ —ā—Ä–Ķ–Ī—É–Ķ—ā –ī–Ľ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ—Ü–Ķ–ī—É—Ä—č –ĺ–Ī—É—á–Ķ–Ĺ–ł—Ź. –ú–ĺ–∂–Ĺ–ĺ —Ā–ļ–į–∑–į—ā—Ć, —á—ā–ĺ —ć—ā–į –Ņ—Ä–ĺ—Ü–Ķ–ī—É—Ä–į –≤ –ī–į–Ĺ–Ĺ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ –≤—č—Ä–ĺ–∂–ī–Ķ–Ĺ–į.
–ö–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—ā–ĺ—Ä —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā –≤ —Ā–Ķ–Ī–Ķ —É—á–Ķ–Ī–Ĺ—É—é –≤—č–Ī–ĺ—Ä–ļ—É –ī–Ľ—Ź –ļ–į–∂–ī–ĺ–≥–ĺ –ļ–Ľ–į—Ā—Ā–į –ł –ļ–į–∂–ī—č–Ļ –≤—Ö–ĺ–ī –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ —Ā—Ä–į–≤–Ĺ–ł–≤–į–Ķ—ā—Ā—Ź —Ā —ć—ā–ł–ľ–ł –Ĺ–į–Ī–ĺ—Ä–į–ľ–ł –Ņ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ–ĺ–ľ—É –į–Ľ–≥–ĺ—Ä–ł—ā–ľ—É, –ī–į–Ľ–Ķ–Ķ –≤—č–Ī–ł—Ä–į–Ķ—ā—Ā—Ź –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ—č–Ļ –ļ–Ľ–į—Ā—Ā.
2 –ü—Ä–ł–Ĺ—Ü–ł–Ņ –ľ–į–ļ—Ā–ł–ľ—É–ľ–į –į–Ņ–ĺ—Ā—ā–Ķ—Ä–ł–ĺ—Ä–Ĺ–ĺ–Ļ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ —É—á–Ķ–Ī–Ĺ—č—Ö –Ņ—Ä–ł–ľ–Ķ—Ä–ĺ–≤ (X,Y ), –∑–ī–Ķ—Ā—Ć X ‚ąč x = (őĺ1,‚Ķ,őĺn) ‚Äď –ĺ–Ī—ä–Ķ–ļ—ā—č, Y ‚Äď –ļ–Ľ–į—Ā—Ā—č. –ö–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—ā–ĺ—Ä –ī–ĺ–Ľ–∂–Ķ–Ĺ –ĺ—ā–ĺ–Ī—Ä–į–∂–į—ā—Ć –ĺ–Ī—ä–Ķ–ļ—ā—č –≤ –ļ–Ľ–į—Ā—Ā—č —Ā –ľ–ł–Ĺ–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć—é –ĺ—ą–ł–Ī–ļ–ł
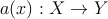
–ü—Ä–ł —ć—ā–ĺ–ľ –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–į–≥–į–Ķ–ľ, —á—ā–ĺ –≤—Ā–Ķ –Ņ—Ä–ł–∑–Ĺ–į–ļ–ł {őĺi} –ĺ–Ī—ä–Ķ–ļ—ā–į –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č –ī—Ä—É–≥ –ĺ—ā –ī—Ä—É–≥–į, –ł–∑-–∑–į —ć—ā–ĺ–≥–ĺ –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł—Ź –Ī–į–Ļ–Ķ—Ā–ĺ–≤—Ā–ļ–ł–Ļ –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—ā–ĺ—Ä –Ĺ–į–∑—č–≤–į—é—ā ‚ÄĚ–Ĺ–į–ł–≤–Ĺ—č–ľ‚ÄĚ.
–Ď–į–Ļ–Ķ—Ā–ĺ–≤—Ā–ļ–ł–Ļ –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—ā–ĺ—Ä –ĺ—Ā–Ĺ–ĺ–≤—č–≤–į–Ķ—ā—Ā—Ź –Ĺ–į –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–Ķ –ľ–į–ļ—Ā–ł–ľ—É–ľ–į –į–Ņ–ĺ—Ā—ā–Ķ—Ä–ł–ĺ—Ä–Ĺ–ĺ–Ļ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł
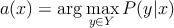
P(y|x) ‚Äď –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć —Ā–ĺ–Ī—č—ā–ł—Ź - x –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–ł—ā –ļ–Ľ–į—Ā—Ā—É y.
–°–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ĺ–Ī –ĺ–Ņ—ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ –Ī–į–Ļ–Ķ—Ā–ĺ–≤—Ā–ļ–ĺ–ľ –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—ā–ĺ—Ä–Ķ[1], a(x) –≤—č–≥–Ľ—Ź–ī–ł—ā —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ
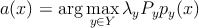 | (1) |
–≥–ī–Ķ őĽy ‚Äď –Ņ–ĺ—ā–Ķ—Ä—Ź –Ņ—Ä–ł –ĺ—ą–ł–Ī–ĺ—á–Ĺ–ĺ–Ļ –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—Ü–ł–ł –ī–Ľ—Ź –ļ–Ľ–į—Ā—Ā–į y, –Ī—É–ī–Ķ–ľ —Ā—á–ł—ā–į—ā—Ć, —á—ā–ĺ –≤ —Ā–Ľ—É—á–į–Ķ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ĺ—ā–≤–Ķ—ā–į –Ņ–ĺ—ā–Ķ—Ä—Ć –Ĺ–Ķ—ā, P(y) ‚Č° Py ‚Äď –į–Ņ—Ä–ł–ĺ—Ä–Ĺ–į—Ź –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć –ļ–Ľ–į—Ā—Ā–į y (–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –ī–ĺ–Ľ–Ķ–Ļ –ĺ–Ī—ä–Ķ–ļ—ā–ĺ–≤ xy –ļ–Ľ–į—Ā—Ā–į y –≤ –ĺ–Ī—Č–Ķ–ľ –Ĺ–į–Ī–ĺ—Ä–Ķ X), py(x) ‚Äď –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā—Ć —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź xy –ł–∑ –ļ–Ľ–į—Ā—Ā–į y.
3 –í–ĺ—Ā—Ā—ā–į–Ĺ–ĺ–≤–Ľ–Ķ–Ĺ–ł–Ķ –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–ł —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź
–Ē–Ľ—Ź –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—ā–ĺ—Ä–į –Ņ–ĺ (1) –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –≤–ĺ—Ā—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā—Ć —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź py –Ņ–ĺ —É—á–Ķ–Ī–Ĺ–ĺ–Ļ –≤—č–Ī–ĺ—Ä–ļ–Ķ (X,Y ). –Ě–Ķ –Ī—É–ī–Ķ–ľ –∑–ī–Ķ—Ā—Ć –ī–Ķ—ā–į–Ľ—Ć–Ĺ–ĺ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ľ–Ķ—ā–ĺ–ī—č –≤–ĺ—Ā—Ā—ā–į–Ĺ–ĺ–≤–Ľ–Ķ–Ĺ–ł—Ź –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–Ķ–Ļ –ł –Ņ—Ä–ł–≤–Ķ–ī—Ď–ľ —Ā—Ä–į–∑—É —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –∑–į–ī–į—á–ł, –Ĺ–ĺ –Ņ—Ä–Ķ–∂–ī–Ķ –ĺ—ā–ľ–Ķ—ā–ł–ľ –≤–į–∂–Ĺ–ĺ–Ķ –ĺ–Ī—Ā—ā–ĺ—Ź—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ. –ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –ľ—č –Ņ—Ä–ł–Ĺ—Ź–Ľ–ł –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł–Ķ –ĺ –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –Ņ—Ä–ł–∑–Ĺ–į–ļ–ĺ–≤ őĺi –ĺ–Ī—ä–Ķ–ļ—ā–ĺ–≤ x ‚ąą X —ā–ĺ –ł—Ā–ļ–ĺ–ľ—É—é n-–ľ–Ķ—Ä–Ĺ—É—é –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā—Ć –ľ–ĺ–∂–Ĺ–ĺ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ–į–ļ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –ĺ–ī–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ—č—Ö –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–Ķ–Ļ.
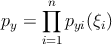
–Ē–Ľ—Ź –≤–ĺ—Ā—Ā—ā–į–Ĺ–ĺ–≤–Ľ–Ķ–Ĺ–ł—Ź –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–ł –Ņ–ĺ –≤—č–Ī–ĺ—Ä–ļ–Ķ –≤–ĺ—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—Ā—Ź –ĺ—Ü–Ķ–Ĺ–ļ–ĺ–Ļ –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–ł –ü–į—Ä–∑–Ķ–Ĺ–į-–†–ĺ–∑–Ķ–Ĺ–Ī–Ľ–į—ā—ā–į[1].
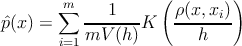
–≥–ī–Ķ m ‚Äď –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤ –≤—č–Ī–ĺ—Ä–ļ–ł X ‚ąč xi, ŌĀ ‚Äď –ľ–Ķ—Ä–į –Ĺ–į X, h ‚Äď –ĺ–ļ—Ä–Ķ—Ā—ā–Ĺ–ĺ—Ā—ā—Ć xi (‚ÄĚ—ą–ł—Ä–ł–Ĺ–į –ĺ–ļ–Ĺ–į‚ÄĚ), K ‚Äď —Ą—É–Ĺ–ļ—Ü–ł—Ź —Ź–ī—Ä–į, V (h) ‚Äď –Ĺ–ĺ—Ä–ľ–ł—Ä—É—é—Č–ł–Ļ –ľ–Ĺ–ĺ–∂–ł—ā–Ķ–Ľ—Ć.
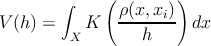
–í –ļ–į—á–Ķ—Ā—ā–≤–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł —Ź–ī—Ä–į –Ī—É–ī–Ķ–ľ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć —Ź–ī—Ä–ĺ –ē–Ņ–į–Ĺ–Ķ—á–Ĺ–ł–ļ–ĺ–≤–į
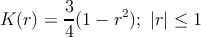 | (2) |
–Ī—É–ī–Ķ–ľ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –ē–≤–ļ–Ľ–ł–ī–ĺ–≤—É –ľ–Ķ—ā—Ä–ł–ļ—É
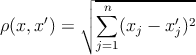 | (3) |
–ē—Č—Ď –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –≤—č–Ī—Ä–į—ā—Ć —ą–ł—Ä–ł–Ĺ—É –ĺ–ļ–Ĺ–į h. –≠—ā–ĺ—ā –Ņ–į—Ä–į–ľ–Ķ—ā—Ä –ľ–ĺ–∂–Ĺ–ĺ –∑–į–ī–į–≤–į—ā—Ć —Ä–į–∑–Ĺ—č–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–ĺ–ľ. –ó–ī–Ķ—Ā—Ć –Ī—É–ī–Ķ–ľ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –ľ–Ķ—ā–ĺ–ī —Ā–ļ–ĺ–Ľ—Ć–∑—Ź—Č–Ķ–≥–ĺ –ļ–ĺ–Ĺ—ā—Ä–ĺ–Ľ—Ź Leave One Out. –ü–į—Ä–į–ľ–Ķ—ā—Ä h –≤—č–Ī–ł—Ä–į–Ķ–ľ –Ņ–Ķ—Ä–Ķ–Ī–ĺ—Ä–ĺ–ľ, –ļ–į–∂–ī—č–Ļ —Ä–į–∑ –Ņ—Ä–ĺ–≤–Ķ—Ä—Ź—Ź —Ā—É–ľ–ľ–į—Ä–Ĺ—É—é –ĺ—ą–ł–Ī–ļ—É –Ĺ–į —É—á–Ķ–Ī–Ĺ–ĺ–ľ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–Ķ, –Ņ—Ä–ł —ć—ā–ĺ–ľ –ł–∑ —É—á–Ķ–Ī–Ĺ–ĺ–≥–ĺ –Ĺ–į–Ī–ĺ—Ä–į —É–ī–į–Ľ—Ź–Ķ—ā—Ā—Ź —ā–Ķ–ļ—É—Č–ł–Ļ (–Ņ—Ä–ĺ–≤–Ķ—Ä—Ź–Ķ–ľ—č–Ļ) –Ņ—Ä–ł–ľ–Ķ—Ä.
![‚ąĎl
LOO (h,X ) = [a(xi;{X ‚ąēxi},h) ‚ĀĄ= yi] ‚Üí min
i=1 h](content/ml-bayes.html/index8x.png)
4 –Ď–į–Ļ–Ķ—Ā–ĺ–≤—Ā–ļ–ł–Ļ –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—ā–ĺ—Ä
–í –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–ľ –ł—ā–ĺ–≥–Ķ –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—ā–ĺ—Ä –ĺ–Ņ–ł—Ā—č–≤–į–Ķ—ā—Ā—Ź —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ–ľ.
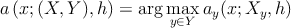
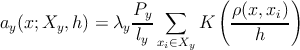
–≥–ī–Ķ (X,Y ) - —É—á–Ķ–Ī–Ĺ–į—Ź –≤—č–Ī–ĺ—Ä–ļ–į, őĽy - –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā –Ņ–ĺ—ā–Ķ—Ä—Ć –Ĺ–į –ļ–Ľ–į—Ā—Ā–Ķ y, Py - –į–Ņ—Ä–ł–ĺ—Ä–Ĺ–į—Ź –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć y, ly - –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –ĺ–Ī—ä–Ķ–ļ—ā–ĺ–≤ x –≤ –ļ–Ľ–į—Ā—Ā–Ķ y, ŌĀ ‚Äď –ľ–Ķ—Ä–į (3) –Ĺ–į X, K ‚Äď —Ą—É–Ĺ–ļ—Ü–ł—Ź —Ź–ī—Ä–į (2).
 |
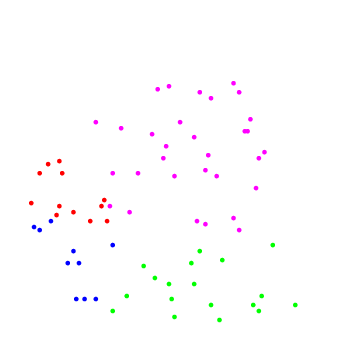 |
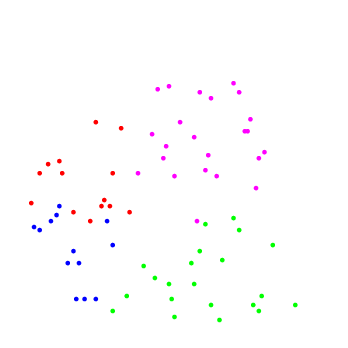
| –†–ł—Ā.1: —É—á–Ķ–Ī–Ĺ—č–Ļ –Ĺ–į–Ī–ĺ—Ä | –†–ł—Ā.2: —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā —Ä–į–Ī–ĺ—ā—č |
–†–Ķ–į–Ľ–ł–∑–į—Ü–ł—Ź –≤ —Ā–ł—Ā—ā–Ķ–ľ–Ķ Octave [ –∑–ī–Ķ—Ā—Ć ].
–°–Ņ–ł—Ā–ĺ–ļ –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä—č
[1] –í–ĺ—Ä–ĺ–Ĺ—Ü–ĺ–≤ –ö.–í. –°—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ł–Ķ –ľ–Ķ—ā–ĺ–ī—č –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—Ü–ł–ł ‚Äď http://shad.yandex.ru/lectures/machine_learning.xml
